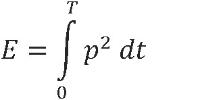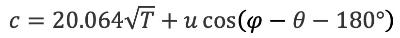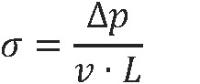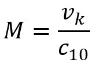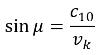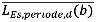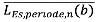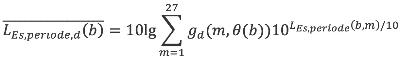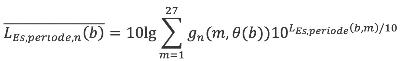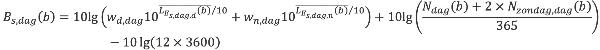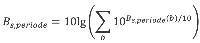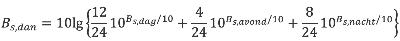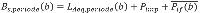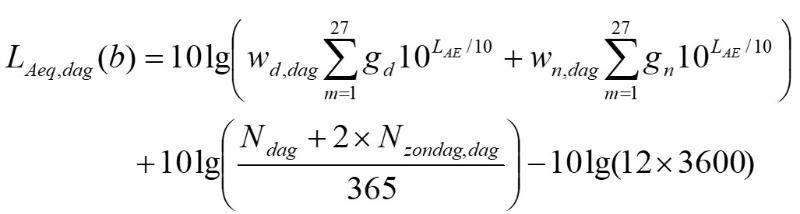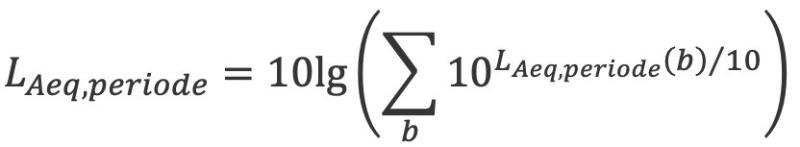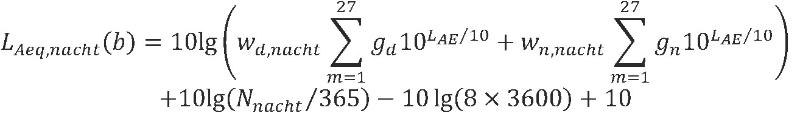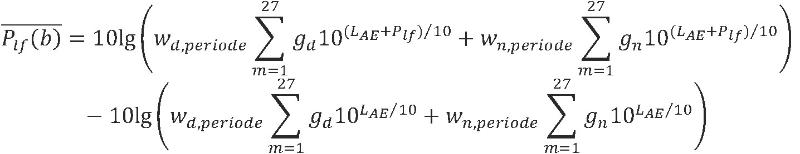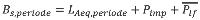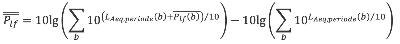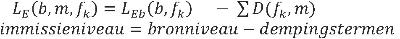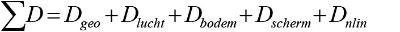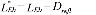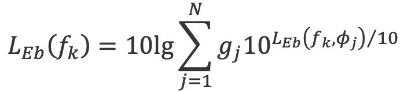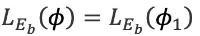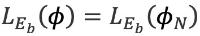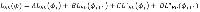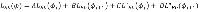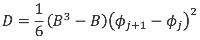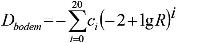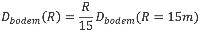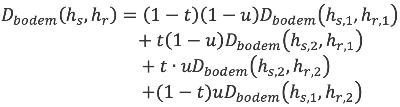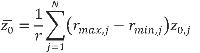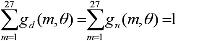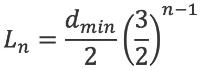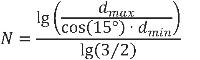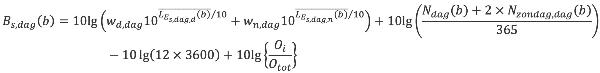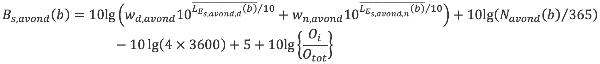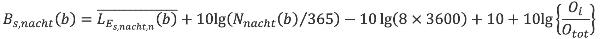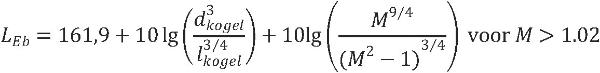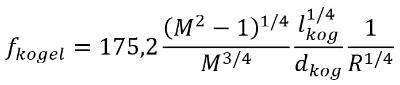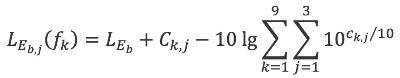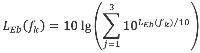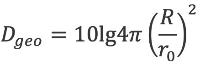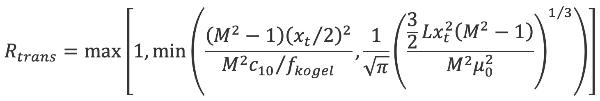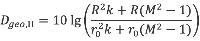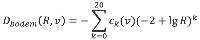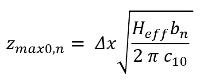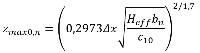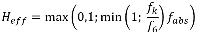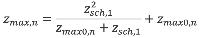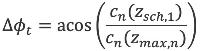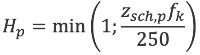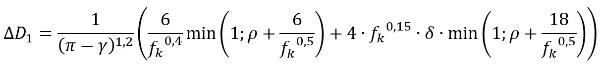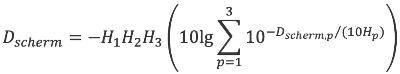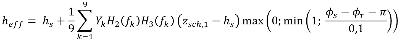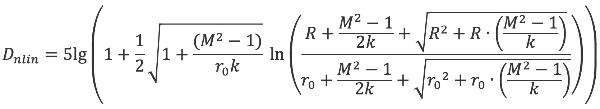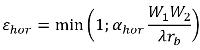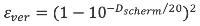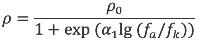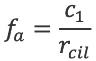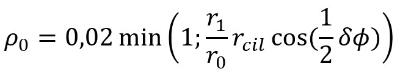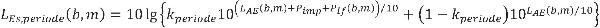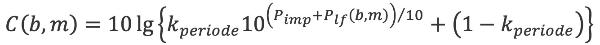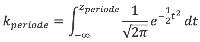Einde inhoudsopgave
Omgevingsregeling
Bijlage XVIIIc
Geldend
Geldend vanaf 01-01-2024
- Bronpublicatie:
14-09-2023, Stcrt. 2023, 26205 (uitgifte: 19-09-2023, regelingnummer: 2023-0000568411)
23-09-2022, Stcrt. 2022, 26085 (uitgifte: 28-09-2022, kamerstukken/regelingnummer: -)
29-06-2021, Stcrt. 2021, 34636 (uitgifte: 01-07-2021, kamerstukken/regelingnummer: -)
19-03-2021, Stcrt. 2021, 15868 (uitgifte: 26-03-2021, kamerstukken/regelingnummer: -)
01-12-2020, Stcrt. 2020, 64380 (uitgifte: 03-12-2020, kamerstukken/regelingnummer: -)
21-11-2019, Stcrt. 2019, 56288 (uitgifte: 22-11-2019, kamerstukken/regelingnummer: -)
- Inwerkingtreding
01-01-2024
- Bronpublicatie inwerkingtreding:
26-09-2023, Stcrt. 2023, 26454 (uitgifte: 02-10-2023, regelingnummer: 2023-0000589458)
19-04-2023, Stcrt. 2023, 11246 (uitgifte: 19-04-2023, kamerstukken/regelingnummer: -)
19-04-2023, Stcrt. 2023, 11246 (uitgifte: 19-04-2023, kamerstukken/regelingnummer: -)
19-04-2023, Stcrt. 2023, 11246 (uitgifte: 19-04-2023, kamerstukken/regelingnummer: -)
19-04-2023, Stcrt. 2023, 11246 (uitgifte: 19-04-2023, kamerstukken/regelingnummer: -)
19-04-2023, Stcrt. 2023, 11246 (uitgifte: 19-04-2023, kamerstukken/regelingnummer: -)
- Overige regelgevende instantie(s)
Ministerie van Economische Zaken en Klimaat
Ministerie van Onderwijs, Cultuur en Wetenschap
Ministerie van Landbouw, Natuur en Voedselkwaliteit
Ministerie van Defensie
- Vakgebied(en)
Milieurecht / Algemeen
Omgevingsrecht / Algemeen
bij de artikelen 6.9, eerste lid, en 8.26, eerste lid, van deze regeling (Rekenmethode geluid civiele buitenschietbanen, militaire buitenschietbanen en militaire springterreinen)
1. Inleiding
Deze rekenmethode is van toepassing op de berekening van het geluid van civiele buitenschietbanen, militaire buitenschietbanen en militaire springterreinen. De rekenmethode bestaat uit deze bijlage in combinatie met vijf gegevensbestanden die voor de rekenmethode worden toegepast. Deze gegevensbestanden zijn niet vrij beschikbaar.
Daarnaast zijn twee programma's nodig: ShowdB en ShowKog. Met het programma ShowdB kunnen de gegevensbestanden worden bekeken en kan de afhankelijkheid van de verschillende parameters die hierbij een rol spelen zichtbaar worden gemaakt. Met het programma ShowKog wordt de uitbreiding van kogel- en mondingsgeluid gevisualiseerd. Deze programma's zijn ook niet algemeen beschikbaar. Verdere achtergrondinformatie en wetenschappelijke onderbouwing is te vinden in handboeken en in onderzoeksrapporten van TNO die bij het Ministerie van Infrastructuur en Waterstaat opvraagbaar zijn.
In bepaalde gevallen kan het geluid van een civiele buitenschietbaan ook worden berekend volgens de eenvoudigere methode beschreven in bijlage XXVIIId. Het gaat om eenvoudige situaties bij kleiduivenbanen en schermenbanen die voldoen aan de in het toepassingsbereik van die bijlage genoemde specificaties.
2. Definities en begrippen
2.1. Schietgeluid
Voorbeelden van schietgeluid zijn schoten met vuurwapens en detonaties van handgranaten, projectielen en bommen. Ook het geluid dat ontstaat bij gebruik van wapen- of knalsimulatoren valt hieronder. Een voorbehoud moet worden gemaakt voor zware vliegtuigbommen, aangezien het frequentiegebied hierbij zo laag is, dat het model vooralsnog niet kan worden toegepast (zie ook paragraaf 4.2).
2.2. Akoestische grootheden
In deze rekenmethode wordt een groot aantal akoestische begrippen gebruikt. In paragraaf 2.10 is een overzicht gegeven van de symbolen, die hiervoor worden gebruikt. Hieronder worden van de belangrijkste begrippen de definities gegeven, die specifiek voor schietgeluid worden gebruikt. Voor de overige akoestische begrippen wordt verwezen naar akoestische handboeken; frequentiewegingen zijn gedefinieerd in IEC 60651.
Momentane geluiddruk: p [Pa]
De (momentane) geluiddruk in een geluidveld is gedefinieerd als de totale druk verminderd met de statische druk. De geluiddruk varieert met de tijd en met de positie.
Geluidexpositie: E [Pa2s]
De geluidexpositie E van een geluidpuls is gedefinieerd als de tijdsintegraal van het kwadraat van de momentane geluiddruk p(t) over de tijdsduur T van de geluidpuls:
| (2.1) |
Hierbij wordt in het algemeen een frequentieweging toegepast op het geluiddruksignaal p(t). In deze rekenmethode worden de A-weging en de C-weging toegepast.
Geluidexpositieniveau: LE[dB(A) of dB(C)]
Het geluidexpositieniveau LE is gedefinieerd als tien keer de logaritme met grondtal 10 van de verhouding van de geluidexpositie E en een referentiewaarde E0 = (20μPa)2s:
LE = 10lg(E/E0) | (2.2) |
De frequentieweging wordt aangegeven door een extra subscript, dus LAE of LCE voor de A-weging resp. de C-weging.
Bronniveau: LEb
Het bronniveau LEb van een puntbron is in deze gedefinieerd als:
LEb = LE + 10lg4πr2 | (2.3) |
waarin LE het geluidexpositieniveau is op een afstand r van de bron in een homogeen verliesvrij medium. In deze rekenmethode wordt gerekend in octaafbanden, en de bronniveaus worden dus per octaafband opgegeven. Deze definitie is alleen van toepassing op mondingsgeluid en detonatiegeluid, die door puntbronnen worden gerepresenteerd. Voor kogelgeluid wordt een andere definitie van het bronniveau gehanteerd (zie paragraaf 4.6.1).
2.3. Meteorologische grootheden
Bij de rekenmethode wordt de (hinder-relevante) geluidbelasting bepaald als een gemiddelde over verschillende meteorologische klassen. Hierbij wordt dus rekening gehouden met het feit dat de geluidoverdracht sterk afhankelijk is van de plaatselijke weersomstandigheden. De verschillende meteorologische klassen worden getypeerd door het effectieve geluidsnelheidsprofiel. In deze paragraaf worden de definities gegeven van de grootheden die hierbij een rol spelen.
Windsnelheid: u [m/s]
De windsnelheid is aan sterke fluctuaties in de tijd onderhevig. Voor een beschrijving van de toestand van de atmosfeer wordt van de gemiddelde windsnelheid uitgegaan, waarbij gemiddeld is over een periode van typerend 5 minuten. De windsnelheid neemt over het algemeen met de hoogte toe. In de rekenmethode wordt ervan uitgegaan dat de gemiddelde windsnelheid in het geluidpad niet met de horizontale positie varieert. Met name bij land-waterovergangen kan dit echter wel het geval zijn. De methode is dan niet zonder meer toepasbaar. In deze rekenmethode wordt alleen de horizontale component van de windsnelheid gebruikt, aangeduid met het symbool u.
Temperatuur: t [°C] en T [K]
De temperatuur is aan fluctuaties in de tijd onderhevig. Voor een beschrijving van de toestand van de atmosfeer wordt van het gemiddelde uitgegaan, waarbij gemiddeld is over een periode van typerend 5 minuten. In de rekenmethode is ervan uitgegaan dat de gemiddelde temperatuur in het geluidpad alleen met de hoogte varieert. Met name bij land-waterovergangen treden ook horizontale temperatuurverschillen op. De methode is dan niet zonder meer toepasbaar. Zowel de temperatuur in graden Celsius als de absolute temperatuur in Kelvin worden gebruikt.
Windrichting: φ [°]
De windrichting is de richting van waaruit de wind komt. De windrichting wordt uitgedrukt in graden ten opzichte van het noorden (kloksgewijs). Westenwind komt dus overeen met 270°.
Effectieve geluidsnelheid: ceff[m/s]
De effectieve geluidsnelheid, dat is de snelheid waarmee een geluidgolf zich in de atmosfeer voortplant, wordt bepaald door de absolute temperatuur T, de horizontale windcomponent u, en het hoekverschil tussen de windrichting φ en de richting θ waarin het geluid zich voortplant (φ en θ zijn hoeken ten opzichte van het geografische noorden; dus bv. φ = 90° voor oostenwind, en θ = 90° voor geluidvoortplanting van west naar oost).
| (2.4) |
De geluidsnelheid is dus gelijk aan de som van de ‘thermische geluidsnelheid’ en de vectorwind, de component van de wind in de geluidvoortplantingsrichting. In deze rekenmethode wordt de aanduiding ‘effectief’ meestal weggelaten, en wordt de ‘effectieve geluidsnelheid’ als de ‘geluidsnelheid’ aangeduid. In overeenstemming hiermee wordt het symbool c gebruikt in plaats van ceff.
Geluidsnelheidsprofiel: c(h) [m/s]
Het verloop van de effectieve geluidsnelheid met de hoogte (h) wordt aangeduid als het geluidsnelheidsprofiel c(h). Dit verloop is een gevolg van de variaties van de temperatuur T en de windsnelheid u met de hoogte. In deze rekenmethode wordt de (hinder-relevante) geluidbelasting berekend als een gewogen gemiddelde over 27 meteorologische klassen. Deze klassen worden getypeerd door het geluidsnelheidsprofiel waarbij drie groepen worden onderscheiden (zie § 4.4.2).
Relatieve vochtigheid: rv [%]
De relatieve vochtigheid van de atmosfeer is gedefinieerd als de partiële druk van waterdamp in de atmosfeer gedeeld door de verzadigings-dampdruk, uitgedrukt als een percentage.
Ruwheidslengte: z0 [m]
Vlakbij de bodem is de windsnelheid vrijwel gelijk aan nul. De ruwheidslengte van de bodem is gedefinieerd als de hoogte waar beneden de windsnelheid gelijk is aan nul. Voor de bepaling van de ruwheidslengte kan gebruik worden gemaakt van de Davenport-classificatie. Volgens deze classificatie bedraagt de ruwheidslengte 0,0002 m voor een wateroppervlak, 0,03 m voor open grasland en 0,25 m voor heide.
Meteorologische dag
Periode tussen één uur na zonsopgang en één uur voor zonsondergang.
Meteorologische nacht
Periode tussen één uur voor zonsondergang en één uur na zonsopgang.
Juridische dag, avond en nacht
Er worden drie beoordelingsperioden onderscheiden:
- •
dagperiode 07.00 – 19.00 uur;
- •
avondperiode 19.00 – 23.00 uur;
- •
nachtperiode 23.00 — 07.00 uur.
Windroossector: [χ,ζ] [°,°]
Gedeelte van de windroos, dat voor het gebruik van de schietbaan relevant is. Van de windroossector wordt de sectorhoek χ gegeven en het midden van de windroossector ζ. Bij een windroossector van bijvoorbeeld [90°, 270°] is het gebruik van de schietbaan alleen relevant bij windrichtingen van (270° ± 45°) wat overeenkomt met windrichtingen tussen noordwest en zuidwest (zie ook figuur 4.4).
2.4. Beoordelingsgrootheden
Geluidbelasting van schietgeluid: Bs[dB(A)]
De hinderrelevante geluidbelasting van schietgeluid wordt aangegeven door het symbool Bs en uitgedrukt in dB(A). De dosis-effect relatie voor hinder van wegverkeersgeluid is hierbij als referentie gekozen. Dit houdt in dat bij gelijke hinderbeleving de getalwaarden van de geluidbelasting van schietgeluid en wegverkeersgeluid aan elkaar gelijk zijn.
In de geluidbelasting is de gemiddelde invloed van het weer op de geluidoverdracht verwerkt.
De geluidbelasting kan worden onderverdeeld in deelgeluidbelastingen van diverse schietactiviteiten. De totale geluidbelasting is de energetische som van deze deelgeluidbelastingen.
In analogie met de beoordelingsprocedures voor wegverkeers- en industriegeluid wordt bij zonering van schietgeluid de geluidbelasting uitgedrukt in een dag-avond-nachtwaarde (Bs,dan), die bepaald wordt als een gewogen gemiddelde van de Bs waarden voor de drie juridische beoordelingsperioden:
- •
Bs,dag dag: 07.00 – 19.00 uur;
- •
Bs,avond avond: 19.00 – 23.00 uur;
- •
Bs,nacht nacht: 23.00 — 07.00 uur.
2.5. Bodemparameters
De bodem wordt akoestisch gekarakteriseerd door twee parameters: de akoestische bodemhardheid en de bodemruwheid.
De akoestische bodemhardheid is bepalend voor reflectie en absorptie van geluid door de bodem. Als maat voor de bodemhardheid wordt de stromingsweerstand σ gehanteerd. De stromingsweerstand wordt gedefinieerd aan de hand van een situatie waarin een luchtstroom door een laag van het materiaal een drukval over de laag veroorzaakt. De stromingsweerstand is dan gelijk aan verhouding van de drukval Δp en de stroomsnelheid v, gedeeld door de laagdikte L. In formule:
| (2.5) |
In deze rekenmethode voor schietgeluid wordt van drie waarden voor de akoestische bodemhardheid uitgegaan: reflecterend, absorberend en zeer absorberend. Voor de stromingsweerstand wordt voor een zeer absorberende bodem en een absorberende bodem respectievelijk 1·105 Nsm−4 en 3·105 Nsm−4gehanteerd. Voor een akoestisch reflecterende bodem wordt een oneindig grote stromingsweerstand aangenomen (zie ook § 4.5.2).
De bodemruwheid beïnvloedt het windsnelheidsprofiel in de atmosfeer boven de bodem, en daardoor indirect de geluidoverdracht. Een maat voor de bodemruwheid is de ruwheidslengte z0 (zie § 2.4).
2.6. Kogelparameters
Voor de berekening van het niveau van het kogelgeluid zijn in eerste instantie twee parameters van belang: de kogeldiameter dkogel gedefinieerd als de maximale diameter van de kogel en de effectieve lengte lkogel gedefinieerd als de axiale afstand van de punt van de kogel tot aan de plaats waar de diameter maximaal is.
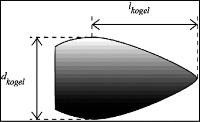
Figuur 2.1: Effectieve lengte lkogel en diameter dkogel van een kogel
Het gebied waar het kogelgeluid kan worden waargenomen hangt af van de snelheid van de kogel. Deze snelheid wordt benaderd door een lineaire relatie:
vk = v0 + v1x | (2.6) |
met
v0 de snelheid van de kogel bij het verlaten van de vuurmond;
v1 de verandering van de snelheid per eenheid van lengte;
x de afstand langs de kogelbaan tot de vuurmond.
Een afgeleide parameter die een rol speelt bij de berekening van kogelgeluid is het Mach-getal. Dit is gedefinieerd als de verhouding van de snelheid vk van de kogel en de geluidsnelheid c10 (hiervoor wordt in deze rekenmethode de waarde bij 10°C en 1 atmosfeer gehanteerd: c10 = 337.6 m/s).
| (2.7) |
2.7. Buitenschietbanen
Op verschillende soorten banen wordt geschoten of andersoortig knalgeluid gemaakt. In onderstaande tabel is een overzicht gegeven met voorbeelden van baantypen die in Nederland voorkomen en die in het kader van deze rekenmethode relevant zijn. Voor het vaststellen van de geluidbelasting vragen de verschillende baantypen om een andere aanpak.
Vrije schietbanen
Dit zijn schietbanen, meestal voorzien van een kogelvanger, en mogelijk een overkapping boven de standplaats van de schutters, maar zonder voorzieningen ter beperking van de omvang van de onveilige zone zoals poorten, kokers, schermen, en dergelijke.
De vrije schietbanen zijn onder te verdelen in:
- •
vrije geweerbanen;
- •
vrije mitrailleurbanen en vrije pistoolbanen.
De lengte van een vrije geweerbaan is doorgaans 300 m; het aantal schietpunten varieert.
In principe bestaat tussen de uitvoering van een vrije mitrailleurbaan en die van een vrije pistoolbaan geen verschil. Een vrije pistoolbaan heeft een lengte van 25m; het aantal schietpunten bedraagt doorgaans vijf tot tien.
Schietkampen
Een schietkamp bestaat uit een of meer schietbanen of schietpunten. De doelafstanden zijn hierbij groter dan bij vrije schietbanen. Deze terreinen beslaan meerdere vierkante kilometers. Afhankelijk van de baan wordt met diverse wapentypen geschoten variërend van lichte handvuurwapens tot 155 mm Houwitsers.
Poortbanen
Dit zijn schietbanen waarbij met poorten en kogelvangers wordt voorkomen dat — bij normaal gebruik — een direct schot de baan kan verlaten, waardoor een zekere mate van veiligheid wordt verkregen en met een beperkte onveilige zone kan worden volstaan. De poortbanen zijn onder te verdelen in geweerpoortbanen en pistoolpoortbanen.
Een geweerpoortbaan heeft bijvoorbeeld een lengte van 100 m, 200 m of 300 m. Een pistoolpoortbaan is 20 m of 25 m lang. Het aantal schietpunten op de banen is meestal zes. Bij pistoolpoortbanen maakt de eerste poort deel uit van een schiethuisje waarin de schutters zich bevinden.
Het geluiduitstralingspatroon van een poortbaan is, door de vele reflecties die mogelijk zijn, zeer complex. Voor de berekening van de geluidbelasting wordt in de rekenmethode deze baan door een puntbron gemodelleerd. Deze beschrijving is pas geldig op enige afstand van deze baan. In paragraaf 4.5.1 wordt hier nader op ingegaan.
Schermenbanen
Dit zijn schietbanen waarbij met schermen, zijwallen of zijwanden en een overkapping boven de kogelvanger wordt voorkomen dat — bij normaal gebruik van de baan — een direct schot of een ricochet de baan kan verlaten, waardoor geen onveilige zone in acht genomen hoeft te worden. De schermenbanen zijn onder te verdelen in schermenbanen voor geweer en schermenbanen voor pistool.
Een schermenbaan voor geweer heeft een lengte van bijvoorbeeld 100 m, 200 m of 300 m. Een schermenbaan voor pistool is 25 m lang. Er zijn op schermenbanen meestal zes schietpunten. Het schuttersgedeelte van de baan is meestal overkapt. Ook zijn er voorbeelden waarbij de schutter, gelegen op een brits, vanuit een omsloten ruimte door een klein venster schiet. Een 100 m baan kan ook voor het schieten met vuistvuurwapens worden gebruikt. De schutter gaat hiertoe naar voren op een afstand van 25 m of minder van de kogelvanger. Deze schietpositie is meestal niet overkapt.
De schermen zijn van beton en bekleed met hout. Akoestisch kunnen deze schermen de geluiduitstraling naar de omgeving sterk beïnvloeden. Naast een geluidreducerende invloed kunnen ze in bepaalde richtingen ook een geluidversterkende invloed hebben door reflectie van het geluid tegen deze schermen. Op schermenbanen waar voldoende aanvullende akoestische maatregelen zijn getroffen, zal buiten de baan alleen kogelgeluid een rol van betekenis spelen.
Het geluiduitstralingspatroon van een schermenbaan is, door de vele reflecties die mogelijk zijn, zeer complex. Voor de berekening van de geluidbelasting wordt in de rekenmethode de schermenbaan gemodelleerd door één of meer puntbronnen. Deze beschrijving is pas geldig op enige afstand van de schermenbaan. In paragraaf 4.5.1 wordt hierop nader op ingegaan.
Poortkokerbanen
Dit zijn schietbanen waarbij met een poort en een koker wordt voorkomen dat — bij normaal gebruik van de baan — een direct schot of een ricochet de baan kan verlaten, waardoor geen onveilige zone in acht genomen hoeft te worden.
Een poortkokerbaan heeft meestal een lengte van 25 m. Het aantal schietpunten bedraagt doorgaans vijf of zes. De schietposities bevinden zich net buiten het gebouw (aan de open zijde) of voor kortere doelafstanden in het gebouw (de kokers zijn groot genoeg om in te staan). De bodem van de schietposities net buiten het gebouw is verlaagd uitgevoerd. Het gebouw is voorzien van een sheddak dat aan dezelfde kant als waar de opening van het gebouw ligt kleine ramen heeft.
Ook een poortkokerbaan wordt in de rekenmethode gemodelleerd door een puntbron. De geluiduitstraling is sterk richtingsafhankelijk. Met name naar achteren toe straalt een poortkokerbaan het meeste geluid uit. Door de afschermende werking van wanden en plafond is de geluiduitstraling lager naarmate het schietpunt dieper in het gebouw ligt.
Kokerbanen
Dit zijn schietbanen waarbij met een koker wordt voorkomen dat — bij normaal gebruik van de baan — een direct schot of een ricochet de baan kan verlaten, waardoor geen onveilige zone in acht genomen hoeft te worden.
Een kokerbaan heeft alleen één open zijde achter de standplaats van de schutters. Een kokerbaan heeft doorgaans een lengte van 25 m. De schietposities bevinden zich bij de open zijde of (voor kortere doelafstanden) in het gebouw. Op een afstand van circa 2 m van de kogelbaan is meestal aan beide kanten een verbreding van circa 0,55 m in de koker aangebracht waarin zich een (niet aanschietbare) deur bevindt. De bodem van de schietposities net buiten het gebouw is meestal verlaagd uitgevoerd. Het gebouw is voorzien van een sheddak dat aan dezelfde kant als waar de opening van het gebouw ligt kleine ramen heeft.
Ook een kokerbaan wordt in de rekenmethode gemodelleerd door een puntbron. De geluiduitstraling is sterk richtingsafhankelijk. Met name naar achteren toe straalt een kokerbaan het meeste geluid uit. Door de afschermende werking van wanden en plafond neemt het bronniveau af als het schietpunt zich meer in het gebouw bevindt.
Handgranatenbanen
Dit zijn banen waar met scherpe handgranaten kan worden geworpen. Een handgranatenbaan bestaat uit een schuilplaats voor de oefenende eenheid, een munitie opslag- en verstrekkingspunt, een werppunt, een waarnemingspunt voor de officier belast met de leiding en een dekkingswal. Voorts behoort tot de baan een geëgaliseerde terreinstrook, breed ten minste 50 m en diep ten minste 75 m, waar de geworpen granaat terecht moet komen.
Miniatuurschietbanen
Dit zijn schietbanen waarbij geschoten wordt met geweren, kaliber .22 inch, bevestigd in of aan boordkanonnen van voertuigen. Een miniatuurschietbaan bestaat meestal uit een verhard opstelplateau voor de voertuigen, een doelengebied van relatief grote omvang, doorgaans aangeduid als ‘zandbak’, en een kogelvanger, al dan niet voorzien van een overkapping.
Banen met schietbomen
Op deze banen wordt er vanaf een vaste standplaats op een schietboom geschoten waarop een doel is aangebracht. Er wordt geschoten met geweren, lucht- of CO2-wapens of kruis- of handbogen. Behalve bij de kruis- en handbogen wordt gebruik gemaakt van een oplegsteun voor het wapen. In enkele gevallen is er ook een kogelvanger aanwezig.
Afhankelijk van het type doel wordt het aangeduid als Oud Limburgs schieten, Brabants schieten of Gelders schieten. Bij Oud Limburgs schieten wordt de hark of de vogel als doel gebruikt. De hark is een houten raamwerk waarop een groot aantal blokjes hout is bevestigd. De vogel is een blok hout in de vorm van een vogel. Bij Brabants schieten wordt op de wip (een stalen schijfje) of op de gaai (vogel) geschoten. Bij Gelders schieten wordt geschoten op de vogel, de schijf of de lepel. Bij het schieten op de schijf wordt een papieren roos gebruikt. Bij het lepelschieten bestaat het doel uit een aantal lepels die kunnen scharnieren en die na een treffer weer overeind gehaald kunnen worden.
Miniatuur kanonbanen
Dit zijn schietbanen waar met miniatuur kanonnen wordt geschoten onder een zeer kleine elevatie (5 graden) op doelen op een afstand van 25 tot 50 m.
Kleiduivenschietbanen
Op kleiduivenschietbanen wordt geschoten met hageljachtgeweren. Het doel is een kleiduif (schijf gebakken klei) die met een hand- of mechanisch gedreven kleiduiven-werpmachine wordt weggeworpen over een afstand van maximaal 80 m.
Kleiduivenschietbanen kunnen in verschillende variaties voorkomen:
- •
Op een skeetbaan werpen twee tegenover elkaar staande machines, die zijn opgesteld in een hoge en een lage toren, de kleiduiven elk in een bepaalde richting. De schutter moet voortdurend langs een halve cirkel, met de twee werpmachines op de hoekpunten, van standplaats wisselen. Er zijn acht verschillende standplaatsen;
- •
Bij een trapbaan staat de werpmachine op een vaste plaats opgesteld en zijn er meestal tien standplaatsen voor de schutter. De afstand van de schietpunten tot de werpmachine is 10 tot 15 m;
- •
Bij een enkelvoudige oefenbaan is er alleen één vaste standplaats voor de schutter. De werpmachine is verplaatsbaar;
- •
Bij een hazenbaan wordt meestal geschoten op een metalen schijf in de vorm van een haas waarop een kleiduif is aangebracht. De haas wordt voortbewogen langs draden of op rails met een snelheid van ongeveer 5 m/s. De schutter staat op 15, 20 of 25 m afstand van het doel.
2.8. Militaire oefenterreinen
Op militaire oefenterreinen wordt niet met een scherpe patroon (‘Ball’) geschoten, maar wordt een losse patroon (‘blank’) toegepast, die over het algemeen minder geluid voortbrengt. Verder wordt soms ook gebruik gemaakt van knalsimulatie-middelen.
Gevechtssituaties worden nagebootst waarbij er sprake is van een aanvallende en een verdedigende partij. Plaats en richting van schieten bij deze oefeningen zijn alleen bij benadering bekend. Het verdient daarom aanbeveling van een referentieoefening uit te gaan. In paragraaf 4.5.1 wordt hier nader op ingegaan.
2.9. Achtergronden bij de fysische modellering van schietgeluid
Bij het geluid dat ontstaat door het gebruik van een vuurwapen kunnen drie verschillende bijdragen worden onderscheiden:
- •
Mondingsgeluid
- •
Detonatiegeluid
- •
Kogelgeluid
In deze paragraaf zullen we de specifieke fysische eigenschappen van schietgeluid nader toelichten om inzicht te geven in de modellering van schietgeluid.
Mondingsgeluid en detonatiegeluid
Door de explosie van de voortdrijvende lading in een projectiel ontstaat er een grote drukpuls. Het hierdoor opgewekte geluidveld laat zich goed beschrijven door een akoestische puntbron met een richtingsafhankelijke geluiduitstraling. Voor lichte vuurwapens is de richtingsafhankelijkheid over het algemeen groter dan bij de zwaardere wapentypen. Het verschil tussen het niveau vóór en achter het wapen kan bij lichte handvuurwapens in de orde van 15 dB zijn.
Het bronpunt voor lichte handvuurwapens ligt aan het einde van de loop. Voor zwaardere wapens ligt het broncentrum iets verder voor de loop (zie hiervoor ook paragraaf 4.5.1). Als op korte afstand van een wapen afschermende objecten staan opgesteld moet hier terdege rekening mee gehouden worden.
Terugstootloze vuurwapens hebben in principe twee bronpunten, één aan de voorkant (in Engels: muzzle blast) en één aan de achterzijde van het wapen (in Engels: breech blast). Het niveau van het bronpunt aan de achterzijde van het wapen is vele malen sterker dan het bronpunt aan de voorzijde van het wapen, zodat in goede benadering van één bronpunt aan de achterzijde van het wapen kan worden uitgegaan.
Het akoestisch model dat in deze rekenmethode wordt beschreven is een lineair model. Op korte afstand van het wapen zijn de geluiddrukniveaus echter dermate hoog dat de geluidoverdracht niet door een lineair model kan worden beschreven. Op enige afstand van de bron zijn de drukniveaus echter zover afgenomen dat een beschrijving door een lineair model wel kan worden toegepast. Dit betekent dat het model niet op korte afstanden van de bron kan worden toegepast (zie ook paragraaf 4.2).
Kogelgeluid
Kogelgeluid heeft een principieel ander gedrag dan mondings- en detonatiegeluid. Het ontstaat door verstoring van de lucht door een supersone kogel. De luchtverstoring is geconcentreerd op een kegelvormig oppervlak, dat zich met de geluidsnelheid vanaf de kogelbaan uitbreidt. Dit oppervlak wordt de Mach-golf genoemd. Op het moment dat de Mach-golf een waarnemer passeert, wordt het als een knal waargenomen. De kogelknal wordt altijd eerder waargenomen dan de mondingsknal. De halve tophoek μ van de kegelvormige Mach-golf wordt de Mach-hoek genoemd. De Mach-hoek wordt bepaald door de geluidsnelheid c10 en de kogelsnelheid vk, volgens de relatie:
| (2.8) |
De kogelsnelheid neemt in het algemeen af langs de kogelbaan, waardoor de Mach-hoek toeneemt (het complement van de Mach-hoek, ξ = 90° − μ neemt dus juist af langs de kogelbaan). Hierdoor is de Mach-golf geen perfect kegeloppervlak, maar een gekromd kegeloppervlak. Dit is geïllustreerd in figuur 2.2.
Bij de modellering van kogelgeluid worden drie gebieden onderscheiden, die aangegeven zijn in figuur 2.2. Het niveau van kogelgeluid is het hoogst in gebied II, het Mach-gebied. Het niveau is aanzienlijk lager in gebied III, maar niet verwaarloosbaar. Het niveau in gebied I is nog lager, en wordt verwaarloosd. In figuur 2.2 is aangenomen dat de kogel nog supersoon is bij het doel. Dat wil zeggen dat de kogelsnelheid bij het doel groter is dan de geluidsnelheid. Het kan ook voorkomen dat de kogel subsoon wordt vóór het bereiken van het doel. De hoek ξ is dan, op het punt waar de kogel subsoon wordt, gelijk aan nul. Gebied II bestrijkt dan het volledige gebied achter het doel; er is dan geen gebied III.
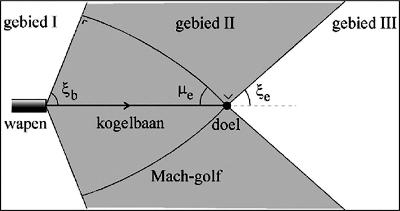
Figuur 2.2: Illustratie van de gebieden I, II en III die worden gebruikt bij de modellering van kogelgeluid. Gebied II wordt het Mach-gebied genoemd. De gekromde lijnen representeren de doorsnede van de (kegelvormige) Mach-golf op het moment dat de kogel het doel bereikt. De Mach-hoek bij het doel is aangegeven als μe.
2.10. Symbolen
Symbool | Eenheid | Omschrijving | Behandeld in |
|---|---|---|---|
α | dB | Constante voor bepalen hinderrelevante geluidbelasting (47 dB) | 3.2 |
αabs | - | Absorptiecoëfficiënt van materialen | 4.6.5 |
αe | ° | Elevatiehoek van de loop van het wapen | 4.4.1 |
β | dB−1 | Constante voor bepalen hinderrelevante geluidbelasting (0,015 dB−1) | 3.2 |
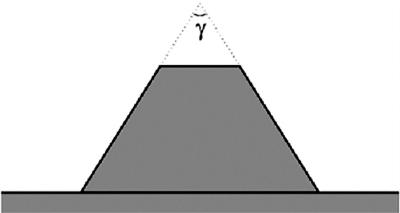
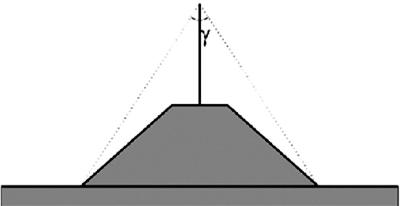
γ | - | Tophoek van wal | 4.5.3 |
εhor | ° | Effectiviteit van de reflectie in het horizontale vlak | 4.6.7 |
εver | - | Effectiviteit van de reflectie in het verticale vlak | 4.6.7 |
ζ | ° | Midden van windroossector, die voor het gebruik van de schietbaan relevant is | 2.3 |
θ | ° | Geluidvoortplantingsrichting t.o.v. het noorden (bijv θ = 90° voor geluidvoortplanting van west naar oost) | 2.3 |
λ | m | Golflengte | 4.6.7 |
μ | ° | Mach-hoek, halve tophoek van de kegel gevormd door het golffront van de Mach-golf | 2.9 |
ξ | ° | Complement van de Mach-hoek | 2.9 |
ξb,ξe | ° | Grenshoeken van het Mach-gebied | 2.9 en 4.6.2 |
ρ | - | Reflectiviteit {reflectiecoëfficiënt voor de geluidenergie (1-αabs)} | 4.5.4 |
σ | kPa s m−2 | Stromingsweerstand | 2.6 en 4.5.2 |
φ | ° | Windrichting (hoek t.o.v. het noorden, bijv. φ = 90° komt overeen met oostenwind) | 2.3 |
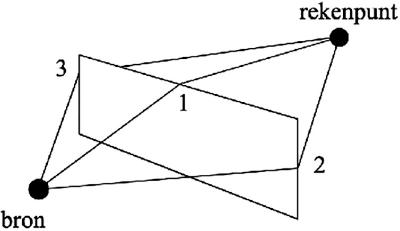
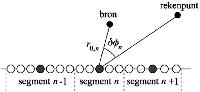
Φ | ° | Hoek tussen de lijn van bron naar rekenpunt en de vuurlijn (in bovenaanzicht vanuit de bron met de klok mee gemeten) | 4.4.1 |
Φr | ° | Diffractiehoek van rekenpunt op top van scherm | 4.6.5 |
Φs | ° | Diffractiehoek van bron op top van scherm | 4.6.5 |
ΔΦr | ° | Correctie op Φr als gevolg van straalkromming | 4.6.5 |
ΔΦs | ° | Correctie op Φs als gevolg van straalkromming | 4.6.5 |
χ | ° | Sectorhoek van windroossector, die voor het gebruik van de schietbaan relevant is | 2.3 |
ψ | ° | Schietrichting t.o.v. het noorden in het horizontale vlak | 4.5.1 |
b | - | Geluidbron | 3.2 en 4.3 |
bn | m/s | Coëfficiënt in formule voor geluidsnelheidsprofielen | 4.4.2 |
Bs | dB(A) | Geluidbelasting van schietgeluid | 2.4 |
Bs,avond | dB(A) | Geluidbelasting in de juridische avondperiode | 2.4 en 3.2 |
Bs,dag | dB(A) | Geluidbelasting in de juridische dagperiode | 2.4 en 3.2 |
Bs,dan | dB(A) | Geluidbelasting uitgedrukt als dag-avond-nachtwaarde | 2.4 en 3.2 |
Bs,nacht | dB(A) | Geluidbelasting in de juridische nachtperiode | 2.4 en 3.2 |
Bs,periode | dB(A) | Geluidbelasting in een bepaalde juridische beoordelingsperiode (dag, avond of nacht) | 3.4 |
c | m/s | Geluidsnelheid | 2.3 |
c(h) | m/s | Geluidsnelheidsprofiel | 2.3 |
c10 | m/s | Geluidsnelheid bij 10°C en 1 atmosfeer (337,6 m/s) | 2.6 |
ceff | m/s | Effectieve geluidsnelheid | 2.3 |
deff | m | Afstand tussen naburige cilinders bij modellering diffuse reflecties | 4.5.4 en 4.6.8 |
dkogel | m | Maximale diameter van kogel | 2.6 |
dmax | m | Maximale afstand van rekenpunt naar rand van brongebied | 4.6.1. |
dmin | m | Minimum afstand van rekenpunt naar rand van brongebied | 4.6.1 |
Dbodem | dB | Demping t.g.v. de bodem | 4.4.2 en 4.6.4 |
Dgeo | dB | Geometrische demping | 4.6.2 |
Dlucht | dB | Demping t.g.v. luchtabsorptie | 4.6.3 |
Dnlin | dB | Extra dempingsterm als gevolg van niet-lineaire geluidoverdracht van kogelgeluid | 4.6.6 |
Drefl | dB | Reflectiedemping | 4.6.7 en 4.6.8 |
Dscherm | dB | Demping door geluidwerende obstakels | 4.6.5 |
ΔD | dB | Tophoekcorrectie | 4.6.5 |
E | Pa2s | Geluidexpositie | 2.2 |
E0 | Pa2s | Referentiewaarde van de geluidexpositie ((20μPa)2s) | 2. |
fa | - | Fractie van het geluidpad waarvoor de bodem absorberend is | 4.6.4 |
fabs | - | Fractie van het geluidpad waarvoor de bodem absorberend of zeer absorberend is | 4.6.5 |
fh | - | Fractie van het geluidpad waarvoor de bodem hard is | 4.6.4 |
fk | Hz | Octaafbandmiddenfrequentie | (fk = 16 Hz, 31,5 Hz, ..., 4000 Hz) |
4 | fz | Fractie van het geluidpad waarvoor de bodem zeer absorberend is | 4.6.4 |
fkogel | Hz | Karakteristieke frequentie van kogelgeluid | 4.6.1 |
gd | - | Gewichtsfactoren voor de meteorologische dag. Dit komt overeen met de kans dat een meteorologische situatie in een bepaalde meteorologische klasse valt. Een meteorologische klasse wordt gekarakteriseerd door één van de 27 geluidsnelheidsprofielen. | 3.2 en 4.4.3 |
gn | - | Gewichtsfactoren voor de meteorologische nacht (zie ook hierboven). | 3.2 en 4.4.3 |
h | m | Hoogte boven het plaatselijk maaiveld | - |
h0 | m | Referentiehoogte (0,1 m) | 4.4.2 |
heff | m | Effectieve hoogte van bronpunt of rekenpunt als gevolg van een scherm | 4.6.5 |
hr | m | Hoogte van het rekenpunt boven het plaatselijke maaiveld | 4 |
hs | m | Hoogte van het bronpunt boven het plaatselijke maaiveld | 4 |
hwapen | m | Hoogte van het draaipunt van de loop van een wapen | 4.4.1 |
Hp | - | Factor waarmee de eindige hoogte en breedte van een scherm in rekening wordt gebracht | 4.6.5 |
kperiode | - | Kans dat schietgeluid in een bepaalde juridische beoordelingsperiode gehoord wordt | 6 |
lkogel | m | Afstand van de punt van de kogel tot aan het punt waar de kogel de grootste diameter heeft | 2.6 |
L | m | Correlatielengte (1,1 m) | 4.6.2 |
LAeq,periode | dB(A) | Equivalente geluidniveau vanwege schietgeluid voor een gemiddelde dag voor een bepaalde juridische beoordelingsperiode | 3.3 |
LE | dB | Geluidexpositieniveau, immissieniveau | 2.2 en 4.3 |
LAE | dB(A) | A-gewogen geluidexpositieniveau | 2.2 |
LCE | dB(C) | C-gewogen geluidexpositieniveau | 2.2 |
LEb | dB | Bronniveau | 2.2 en 4.3 |
L*Eb | dB | Bronniveau van een spiegelbron | 4.3 en 4.6.7 |
LEs,periode(b,m) | dB(A) | Deelbijdrage aan de geluidbelasting van een enkel schot van een bron b bij een meteorologische klasse m. De juridische beoordelingsperiode (dag, avond of nacht) is alleen relevant als een geluidbelasting < 50 dB(A) wordt berekend (zie hoofdstuk 6). | 3.2 |
| dB(A) | Deelbijdrage aan de geluidbelasting voor de meteorologische dag van een enkel schot van een bron b als gewogen gemiddelde over 27 meteorologische klassen. De juridische beoordelingsperiode (dag, avond of nacht) is alleen relevant als een geluidbelasting < 50 dB(A) wordt berekend (zie hoofdstuk 6). | 3.2 |
| dB(A) | Deelbijdrage aan de geluidbelasting voor de meteorologische nacht van een enkel schot van een bron b als gewogen gemiddelde over 27 meteorologische klassen. De juridische beoordelingsperiode (dag, avond of nacht) is alleen relevant als een geluidbelasting < 50 dB(A) wordt berekend (zie hoofdstuk 6). | 3.2 |
Lloop | m | Lengte van de loop vanaf draaipunt tot bronpunt | 4.4.1 |
Ln | m | Breedte van deelgebied van brongebied | 4.6.1 |
m | - | Meteorologische klasse | 3.2, 4.3 en 4.4.2 |
M | - | Mach-getal, relatieve kogelsnelheid ten opzichte van de geluidsnelheid | 2.6 |
n2 | - | Gemiddeld aantal bomen per oppervlakte-eenheid | 4.5.4 en 4.6.8 |
Ncil | - | Aantal cilinders in een segment bij modellering diffuse reflecties | 4.6.8 |
Navond | - | Aantal knallen per jaar in de avondperiode voor een bron | 3.2 |
Ndag | - | Aantal knallen per jaar in de dagperiode (inclusief zon- en feestdagen) | 3.2 |
Nnacht | - | Aantal knallen per jaar in de nachtperiode voor een bron | 3.2 |
Nv | - | Aantal gebieden dat door het geluidpad wordt doorkruist met bodemtype v=h | 4.6.4 |
Nzondag,dag | - | Aantal knallen per jaar in de dagperiode op zon- en feestdagen | 3.2 |
Oi | - | Deeloppervlak van het brongebied | 4.6.1 |
Otot | - | Totale oppervlak van het brongebied | 4.6.1 |
p | Pa | Momentane geluiddruk | 2.2 |
Pimp | dB | Toeslag voor het impulsmatig karakter van het schietgeluid | 3.3 |
Plf | dB | Toeslag voor laagfrequente componenten in het schietgeluid | 3.3 |
Pperiode | - | Aantal dagen per jaar dat op de schietbaan wordt geschoten in een bepaalde juridische beoordelingsperiode (dag, avond of nacht), onafhankelijk van het wapen | 3.4 |
r | m | Afstand | - |
rb | m | Afstand van de bron tot het reflectiepunt | 4.6.7 |
rcil | m | Straal van cilinders bij modellering diffuse reflecties. | 4.5.4 en 4.6.8 |
rv | % | Relatieve vochtigheid | 2.3 |
R | m | Horizontale afstand van bronpunt naar rekenpunt gemeten langs geluidpad | 4 |
Rtrans | m | Afstand van waaraf turbulentie significante invloed heeft op de coherentie van de als lijnbron te beschouwen kogelbaan | 4.6.2 |
R1 | m | Afstand van de doelpositie naar een punt op de grens van het Mach-gebied dat het dichtst bij het rekenpunt ligt | 4.6.2 |
R2 | m | Afstand van het rekenpunt tot de grens van het Mach-gebied | 4.6.2 |
sv | m | Totale horizontale afstand waarover het geluidpad door een bodemgebied met bodemtype v loopt | 4.6.4 |
t | °C | Temperatuur in graden Celsius | 2.3 |
T | K | Temperatuur in Kelvin | 2.3 |
u | m/s | Horizontale windsnelheid | 2.3 |
v0 | m/s | Beginsnelheid van de kogel | 2.6 |
v1 | s−s | Verandering van de kogelsnelheid per meter afgelegde kogelbaan: vk = v0 + v1x | 2.6 |
ve | m/s | Eindsnelheid van de kogel | 4.6.2 |
vk | m/s | Snelheid van de kogel | 2.6 |
wd,periode | - | Fractie van de tijd dat het in een bepaalde beoordelingsperiode een meteorologische dag is | 3.2 |
wn,periode | - | Fractie van de tijd dat het in een bepaalde beoordelingsperiode een meteorologische nacht is | 3.2 |
x | m | Afstand langs de kogelbaan tot de vuurmond | 2.6 |
xr | m | X-coördinaat van het rekenpunt | 4 |
xs | m | X-coördinaat van het bronpunt | 4 |
xt | m | Lengte van de kogelbaan waar het projectiel een supersone snelheid heeft | 4.6.2 |
yr | m | X-coördinaat van het rekenpunt | 4 |
ys | m | Y-coördinaat van het bronpunt | 4 |
z | m | Hoogte van een object t.o.v. een referentievlak | 4 |
z0 | m | Ruwheidslengte van de bodem | 2.3 |
zsch,1 | m | Hoogte van het scherm t.o.v. het maaiveld | 4.6.5 |
zmax | m | Maximale hoogte van geluidstraal | 4.6.5 |
3. Beoordelingsgrootheid
3.1. Inleiding
De geluidbelasting door schietgeluid wordt bepaald uit een combinatie van A- en C-gewogen geluidexpositieniveaus voor een verzameling van 27 meteorologische klassen. Dit is een representatieve deelverzameling van de complexe verzameling van meteorologische situaties, die gedurende een (gemiddeld) jaar kunnen voorkomen. In hoofdstuk 4 wordt beschreven hoe deze geluidexpositieniveaus worden berekend. In dit hoofdstuk is beschreven hoe hieruit de geluidbelasting Bs wordt bepaald, als hinder-relevante beoordelingsmaat voor schietgeluid.
Door uit te gaan van een verzameling van meteorologische klassen kan met het model onder andere onderscheid worden gemaakt tussen de verschillen in geluidoverdracht gedurende de meteorologische dag en nacht en is het model ook toepasbaar in situaties waarin het gebruik van schietbanen gerelateerd is aan de windrichting. Bij de bepaling van de geluidbelasting wordt bovendien het effect van de asymmetrische windroos in rekening gebracht.
In de formules voor de berekening van de geluidbelasting zijn de toeslagen van respectievelijk 5 dB en 10 dB voor de avond en nacht reeds verwerkt. Daarnaast is voor de dagperiode van de zondag een toeslag van 5 dB gehanteerd om voor de extra hinder van schieten op de zondag te verdisconteren. Deze toeslag is op een eenvoudige manier in de formule verwerkt door voor de berekening van de dagperiode het aantal schoten op de zondagen met een factor drie te verhogen.
3.2. Geluidbelasting
In eerste instantie wordt per bron en per meteorologische klasse voor een enkel schot de deelbijdrage bepaald aan de geluidbelasting. Mondingsgeluid, kogelgeluid en detonatiegeluid worden, voor zover hier sprake van is, als bijdragen van afzonderlijke bronnen beschouwd. Voor een meteorologische klasse (m = 1, ..., 27) en bron b wordt deze bijdrage gegeven volgens de formule:
LEs,periode(b,m) = LAE(b,m) + Pimp + Plf(b,m) | (3.1) |
In formule 3.1 is een afhankelijkheid aangegeven van de juridische periode (dag, avond en nacht) waarin een schot wordt afgevuurd. Deze afhankelijkheid is alleen van toepassing als de kans op hoorbaarheid in een periode van invloed is (zie hiervoor hoofdstuk 6)
In bovenstaande formule zijn de volgende toeslagen opgenomen:
- •
toeslag Pimp voor het impulsmatig karakter van schietgeluid:
Pimp= 12 dB
- •
toeslag Plf voor laagfrequente componenten in het schietgeluid:
Plf(b,m) = βΔL'(LAE(b,m) − α)
waarin
α = 47 dB en β = 0,015 dB−1
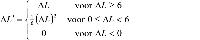
en
ΔL = [LCE(b,m) − LAE(b,m)].
Als er een kans is dat veel bronnen wegvallen in het achtergrondgeluid, maar door het grote aantal schoten (typerend > 1.000.000 schoten op jaarbasis) er toch een relatief hoge geluidbelasting wordt berekend, kan de geluidbelasting op een aangepaste manier worden berekend. Hierbij wordt de impulstoeslag (Pimp=12 dB) en de toeslag voor extra laagfrequente componenten in het geluid (Plf(b,m)) bij de berekening van de geluidbelasting alleen meegenomen voor zover het geluid waarneembaar is op het immissiepunt. In hoofdstuk 6 is deze aangepaste methode beschreven. De aangepaste methode kan alleen worden toegepast als de berekende geluidbelasting met de standaard rekenmethode in een bepaalde periode (dag, avond of nacht) een waarde geeft die lager is dan 50 dB. Toepassing van deze aangepaste methode geeft altijd een lagere waarde.
Per bron worden vervolgens voor zowel de meteorologische dag als de meteorologische nacht (zie formule 3.2 en 3.3) de deelbijdragen aan de geluidbelasting gemiddeld over alle meteorologische klassen. Dit gemiddelde is een gewogen gemiddelde, de gewichtsfactoren (gd en gn voor respectievelijk de meteorologische dag en nacht) staan beschreven in § 4.4.3. Deze gewichtsfactoren zijn onder andere afhankelijk van de ligging van het rekenpunt ten opzichte van de bron. Hiermee wordt verdisconteerd dat de windroos niet rond is (in Nederland overheersen westelijke windrichtingen). Deze afhankelijkheid wordt beschreven als functie van de hoek θ(b) die de lijn van bron naar rekenpunt maakt met het geografische noorden. Voor de meteorologische dag geldt:
| (3.2) |
en voor de meteorologische nacht:
| (3.3) |
Voor de beoordeling van schietgeluid worden drie juridische beoordelingsperioden onderscheiden: dag, avond en nacht (zie § 2.5). De grenzen van deze juridische perioden vallen niet samen met de grenzen van de twee meteorologische perioden: de meteorologische dag en de meteorologische nacht. Hier moet rekening mee worden gehouden bij de berekening van de geluidbelasting voor de drie juridische perioden. Hiertoe wordt gebruik gemaakt van de fracties wd,dag en wn,dag, die aangeven welk gedeelte van de juridische dagperiode (gemiddeld) samenvalt met respectievelijk de meteorologische dag en de meteorologische nacht. Voor de juridische avondperiode worden analoog de fracties wd,avond en wn,avond gebruikt.
Voor de juridische nacht geldt dat deze (gemiddeld) vrijwel volledig binnen de meteorologische nacht valt. De fracties zijn in tabel 3.1 gegeven.
Voor de drie (juridische) beoordelingsperioden wordt voor een bron b de geluidbelasting bepaald volgens de formule:
| (3.4) |
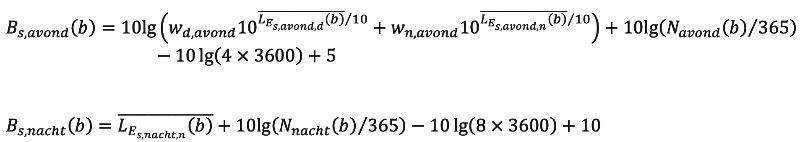
waarin
wd,periode weegfactor voor de meteorologische dag (zie tabel 3.1)
wn,periode weegfactor voor de meteorologische nacht (zie tabel 3.1)
Ndag aantal knallen per jaar in de dagperiode (inclusief zon- en feestdagen)
Nzondag,dag aantal knallen per jaar in de dagperiode op zon- en feestdagen
Navond aantal knallen per jaar in de avondperiode
Nnacht aantal knallen per jaar in de nachtperiode
Tabel 3.1 Fracties (wd,periode en wn,periode) van de tijd dat het in de verschillende beoordelingsperioden een meteorologische dag respectievelijk nacht is.
Periode | Meteorologische dag | Meteorologische nacht |
|---|---|---|
dag | wd,dag = 0,80 | wn,dag = 0,20 |
avond | wd,avond = 0,15 | wn,avond = 0,85 |
nacht | wd,nacht = 0 | wn,nacht = 1 |
De totale geluidbelasting voor een bepaalde beoordelingsperiode wordt bepaald volgens de formule:
| (3.5) |
Bij deze som worden de afzonderlijke geluidcomponenten van een bron (mondingsgeluid, kogelgeluid en detonatiegeluid en hun reflecties) voor zover deze relevant zijn, als afzonderlijke bronnen beschouwd.
De dag-avond-nachtwaarde wordt bepaald door de geluidbelastingswaarden van de drie beoordelingsperioden energetisch bij elkaar op te tellen, waarbij rekening moet worden gehouden met de duur van de periode, volgens de formule:
| (3.6) |
3.3. Bepaling gemiddelde toeslag voor laagfrequente componenten
Om voor een bepaalde juridische beoordelingsperiode een gemiddelde toeslag voor laagfrequente componenten in het schietgeluid te bepalen, wordt de deelbijdrage aan de geluidbelasting voor een bepaalde bron geschreven als:
| (3.7) |
hierin is LAeq,periode (b) het equivalente geluidniveau vanwege schietgeluid voor één bron voor een gemiddelde dag voor een bepaalde juridische beoordelingsperiode en
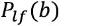
de bijbehorende laagfrequente toeslag, gemiddeld over alle meteorologische klassen.
Deze grootheden kunnen volgens onderstaande formules worden bepaald (voor de overzichtelijkheid zijn in de formules de afhankelijkheden van b en m niet weergegeven):
| (3.8) |
| (3.9) |
Als een toeslag ook als gemiddelde over alle bronnen moet worden bepaald, moeten onderstaande formules worden toegepast:
| (3.10) |
| (3.11) |
| (3.12) |
3.4. Incidenteel gebruik
Als op een schietbaan op minder dan 30 dagen/jaar wordt geschoten moet op Bs,periode een correctie van 10 lg (30/Pperiode) worden toegepast. Pperiode staat voor het aantal dagen per jaar dat op de schietbaan, onafhankelijk van het wapentype, in een bepaalde juridische beoordelingsperiode wordt geschoten.
De geluidbelasting voor een bepaalde juridische beoordelingsperiode Bs,periode wordt dan (als Pperiode< 30) bepaald volgens de formule:
| (3.13) |
3.5. Salvo's
Omdat bij de meeste machinegeweren de knallen binnen een salvo nog afzonderlijk te horen zijn, is ter bepaling van de geluidbelasting ook bij deze wapens de algemene procedure van toepassing. Er bestaan echter ook wapens waarvan de repeteerfrequentie zo hoog is (meer dan 25 schoten per seconde) dat de knallen niet meer afzonderlijk hoorbaar zijn. Ook dan wordt de geluidbelasting berekend op basis van het totaal aantal verschoten patronen binnen de salvo's.
4. Rekenmethode
4.1. Inleiding
In hoofdstuk 3 is beschreven hoe de hinderrelevante beoordelingsmaat voor schietgeluid, de geluidbelasting Bs, berekend wordt op basis van de A- en C-gewogen geluidexpositieniveaus van alle relevante schietgeluidbronnen, voor een verzameling van 27 meteorologische klassen. De berekening van deze geluidexpositieniveaus wordt in dit hoofdstuk beschreven.
4.2. Toepassingsbereik
Aan het toepassingsbereik van de methode zijn grenzen gesteld, die een gevolg zijn van keuzes, die bij de ontwikkeling van deze methode gemaakt zijn.
Voor de afstand tussen bron en rekenpunt is een bovengrens bepaald op 15 km. Voor grotere afstanden is de geluidbelasting van de in Nederland gebruikte wapentypen dermate laag dat berekening niet meer relevant wordt geacht. De gegevensbestanden die horen bij deze methode zijn daarom tot ten hoogste deze afstand toepasbaar.
De ondergrens in afstand wordt door verschillende factoren bepaald. Uitgangspunt is dat het model toegepast wordt voor de berekening van de geluidbelasting rond schietbanen. Bij de ontwikkeling van het model is er daarom vanuit gegaan dat op afstanden korter dan 50 m van het wapen geen geluidniveaus hoeven te worden berekend. Daarnaast wordt de ondergrens bepaald door de eis dat de rekenmethode alleen kan worden toegepast voor het gebied waar de geluidoverdracht door een lineair model kan worden beschreven. Voor zware wapens ligt de ondergrens hierdoor verder weg dan voor lichte wapens. Tot slot wordt de ondergrens ook bepaald door de afmetingen van een bron. Denk hierbij bijvoorbeeld aan een schermenbaan of een deel van een oefengebied. In deze methode worden deze complexe bronnen door een of meer bronnen gemodelleerd. Deze beschrijving is echter pas op enige afstand geldig.
Ook aan het frequentiebereik zijn grenzen gesteld. De rekenmethode is alleen toepasbaar als de relevante geluidenergie beperkt is tot het frequentiegebied lopend van de 16 Hz tot de 4000 Hz octaafband. Voor de in Nederland toegepaste wapentypen kan hiervan worden uitgegaan. Voor exceptionele gevallen (bijvoorbeeld zware vliegtuigbommen) kunnen nog lagere frequenties een belangrijke rol spelen. De methode is dan niet zonder meer toepasbaar.
Een uitgangspunt van de rekenmethode is ook dat de toestand van de atmosfeer in het gebied tussen bron en rekenpunt niet afhangt van de positie. In de meeste situaties in de praktijk wordt hier in goede benadering aan voldaan, maar er zijn uitzonderingen. Zo kan bijvoorbeeld de meteorologische situatie in het Waddenzeegebied en kustgebieden zeer complex zijn. Door temperatuurverschillen tussen land en water ontstaan zogenaamde zeewindverschijnselen. De windrichting en -snelheid en ook de temperatuur zullen dan van plaats tot plaats anders zijn. De methode is in deze bijzondere situaties niet zonder meer toepasbaar.
In theorie zou men zich een schietoefening kunnen voorstellen waarbij ongebruikelijk hoge geluidniveaus optreden. Het is echter niet nodig om grenswaarden aan het geluidexpositieniveau te stellen, omdat bij toepassing van de beoordelingsmethode onmiddellijk blijkt dat zo'n oefening ook een hoge geluidbelasting geeft.
4.3. Principe van de rekenmethode
Uitgangspunt van de methode is de relatie:
| (4.1) |
Per rekenpunt wordt per bron (index b), per octaafband (fk) en voor een verzameling van 27 meteorologische klassen (index m) de geluidimmissie volgens deze relatie bepaald. Zowel het geluidimmissieniveau als het bronniveau worden hierbij als geluidexpositieniveau uitgedrukt. Uit het octaafbandspectrum LE(b,m,fk) worden het A-gewogen immissieniveau LAE(b,m) en het C-gewogen immissieniveau LCE(b,m) berekend. Deze niveaus vormen de basis voor de berekening van de hinderrelevante beoordelingsmaat voor schietgeluid, de geluidbelasting Bs, zoals beschreven in hoofdstuk 3.
De dempingstermen die in het model worden gebruikt zijn:
| (4.2) |
waarbij wordt verstaan onder:
Dgeo geometrische demping;
Dlucht(fk) demping t.g.v. luchtabsorptie;
Dbodem(fk,m) demping t.g.v. de bodem;
Dscherm(fk m) demping door geluidwerende obstakels;
Dnlin extra dempingsterm als gevolg van niet-lineaire geluidoverdracht van kogelgeluid.
Zowel de bodemdemping Dbodem als de schermwerking Dscherm zijn afhankelijk van de meteorologische klasse m. De bodemdemping Dbodem is gedefinieerd als de totale demping in een situatie zonder afschermende objecten, verminderd met Dgeo, Dlucht en Dnlin. Met de term Dscherm wordt de extra demping beschreven van een afschermend object. Hierbij moet worden opgemerkt dat ook de bodemdemping wordt beïnvloed door de aanwezigheid van het afschermende object (namelijk via de effectieve hoogte van de bron of het rekenpunt; zie paragraaf 4.6.5). Dscherm is dus niet gelijk aan de tussenschakelverzwakking van het afschermende object.
Dnlin is alleen van toepassing voor de berekening van de geluidbelasting door kogelgeluid.
Reflecties van mondingsgeluid, kogelgeluid en detonatiegeluid worden als afzonderlijke bronnen beschouwd. Er worden hierbij twee soorten reflecties onderscheiden: spiegelreflecties en diffuse reflecties.
Spiegelreflecties treden op aan verticale of bijna verticale vlakken, bijvoorbeeld een muur of een scherm; de hoek tussen het vlak en de verticaal moet kleiner dan 10° zijn, anders wordt de spiegelreflectie niet meegerekend. Spiegelreflecties worden gemodelleerd met spiegelbronnen. Een reflectie aan een vlak draagt alleen aan het immissieniveau bij als een optische spiegeling van de bron naar het rekenpunt via dat vlak mogelijk is. Er wordt hierbij geen rekening gehouden met kromming van geluidstralen. Het bronniveau van een spiegelbron L*Eb is lager dan het bronniveau van de originele bron; het wordt bepaald uit het bronniveau LEb van de originele bron volgens de formule:
| (4.3) |
waarin LEb het bronniveau (per octaafband) van de originele bron in de richting van het reflectiepunt is en Drefl de reflectiedemping.
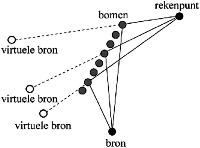
Diffuse reflecties treden op aan een bosrand; als er minder dan drie bomenrijen aanwezig zijn wordt de diffuse reflectie niet meegerekend. Een diffuse reflectie treedt op als er ‘zicht’ is op de bosrand vanuit zowel de positie van de bron als de positie van het rekenpunt; optische spiegeling is hierbij irrelevant. Diffuse reflecties worden gemodelleerd met behulp van virtuele bronnen. Over het algemeen worden er per diffuus reflecterend vlak verschillende virtuele bronnen onderscheiden, dit in tegenstelling tot spiegelreflecties waarbij een reflectie aan een vlak door één spiegelbron wordt gemodelleerd. De bijdragen van de virtuele bronnen aan het totale geluidniveau op het rekenpunt kunnen als incoherent worden beschouwd, zodat elke virtuele bron als een aparte bron kan worden behandeld. Net als bij spiegelreflecties wordt door een reflectiedemping Drefl rekening gehouden met het feit dat het bronniveau van een virtuele bron lager is dan dat van de originele bron. Ook hierbij wordt gebruik gemaakt van formule 4.3.
Meervoudige reflecties worden verwaarloosd. Er treedt dus ten hoogste één spiegelreflectie of diffuse reflectie op langs een geluidpad van de bron naar het rekenpunt. Er kunnen wel verschillende geluidpaden met een reflectie optreden.
Voor de berekening van de geluidbelasting wordt gebruik gemaakt van vijf verschillende gegevensbestanden:
- •
gegevensbestand met brongegevens en andere bronparameters;
- •
gegevensbestand voor het bepalen van de bodemdemping Dbodem;
- •
gegevensbestanden voor het bepalen van de statistische gewichten van de 27 meteorologische klassen.
In principe wordt voor de berekening van de geluidbelasting van zowel mondingsgeluid, detonatiegeluid als kogelgeluid van dezelfde basisformule (4.1) uitgegaan. Het onderscheid zit hem in de manier waarop de verschillende dempingstermen worden berekend. In de volgende paragrafen worden de verschillende onderdelen van de berekeningsmethode in detail besproken. Waar er verschillen zijn tussen de berekening van mondingsgeluid en kogelgeluid, worden deze per onderdeel behandeld.
Ook voor kogelgeluid wordt de berekening uitgevoerd alsof het geluid van een puntbron afkomstig is. Het opmerkelijke bij kogelgeluid is, dat hierbij de bronniveaus rekentechnisch worden vastgesteld (zie § 4.6.1). Dit in tegenstelling tot mondingsgeluid, waarvan de bronsterkte uit metingen is bepaald. Kenmerkend voor kogelgeluid is daarnaast dat dit alleen in bepaalde gebieden waarneembaar is. Drie gebieden worden onderscheiden waarvoor andere berekeningsmethoden worden gehanteerd. Dit komt onder andere naar voren in de manier waarop de geometrische demping bepaald wordt.
Voor de berekening van de luchtdemping wordt eerst het bronspectrum van het mondingsgeluid (dat uit octaafbanden bestaat), geconverteerd naar een tertsband-bronspectrum. Voor kogelgeluid is deze conversie niet nodig omdat de bronsterkte hiervan al in tertsen wordt bepaald.
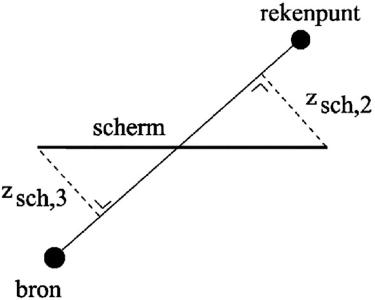
Voor de berekening van de afscherming worden drie bijdragen bepaald via verschillende paden; via één verticaal pad en via twee horizontale paden om het scherm heen. Voor de hiervoor genoemde drie brontypen is de berekeningsmethode gelijk, echter voor kogelgeluid zijn de horizontale paden anders gedefinieerd (zie figuur 4.12). Voor de bodemdemping wordt voor mondingsgeluid, detonatiegeluid en kogelgeluid van dezelfde berekeningsmethode uitgegaan, waarbij bij kogelgeluid — als dit is afgeschermd — de horizontale paden en het verticale pad elk een ander bronpunt kunnen hebben. Tot slot wordt ook voor de berekening van de reflectiebijdrage voor kogelgeluid een aangepaste methode toegepast.
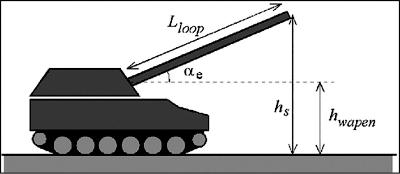
Figuur 4.1: Met de parameters hwapen en Lloop kan de hoogte hs van het bronpunt van de mondingsknal worden berekend voor een gegeven elevatiehoek αe. In deze afbeelding valt het bronpunt samen met de vuurmond, maar in het algemeen kan het bronpunt op enige afstand van de vuurmond liggen. Lloop is dan langer dan de feitelijke lengte van de loop (zie § 4.5.1).
4.4. Toe te passen gegevensbestanden
4.4.1. Gegevensbestanden van bronnen
Een gegevensbestand van schietgeluid-bronnen bevat gegevens van een groot aantal wapen-munitie-gebruikssituatie combinaties. Voor elke combinatie bevat het bestand achtereenvolgens de volgende elementen:
- •
Richtingsafhankelijke bronniveaus voor de verschillende octaafbanden van het mondings- of detonatiegeluid voor wapen-munitie combinaties, die in Nederland voor een bepaalde gebruikssituatie (vrije veld of bijvoorbeeld op een schermenbaan) worden gebruikt. Een verdere beschrijving wordt onder deze opsomming gegeven.
- •
Hoogte van wapen (hwapen) en lengte van de loop (Lloop) in [m] (zie ook figuur 4.1). Deze grootheden zijn hierbij zo gedefinieerd, dat bij een gegeven elevatiehoek αe van de loop van het wapen, de hoogte van het bronpunt boven het plaatselijk maaiveld (hs) bepaald wordt volgens de formule:
hs = hwapen + Lloopsinαe-
(4.4)
- •
Specificatie van de munitie (met bijbehorende aandrijvende lading) of NOV-code van de munitie.
- •
Als het projectiel de loop supersoon verlaat bevat het gegevensbestand bovendien:
- ○
Lengte van de kogel (lkogel) van punt van kogel tot zijn grootste diameter [mm] (zie figuur 2.1);
- ○
Maximale diameter van de kogel (dkogel) [mm];
- ○
Beginsnelheid (v0) van de kogel [m/s];
- ○
Verandering van de kogelsnelheid (v1) per meter afgelegde weglengte [1/s].
Deze parameters worden gebruikt voor de berekening van het bronniveau van kogelgeluid (zie paragraaf 4.6.1). De kogelsnelheid vk op een afstand x van de mond van het wapen wordt gegeven door de relatie:
vk = v0 + v1x | (4.5) |
Voor hand- en vuistvuurwapens kan het aantal wapen-munitiecombinaties dat op een schietbaan wordt gebruikt zo groot zijn dat het een onevenredige inspanning is om voor al deze combinaties de geluidbronsterkte vast te stellen. Hiertoe zijn een aantal standaard categorieën met bijbehorende bronsterkte gedefinieerd, die kunnen worden gebruikt als geen bronsterktemetingen voor die wapen-munitiecombinatie beschikbaar zijn. Deze categorieën zijn beschreven in de Toelichting op toepassing van methoden voor meten en rekenen aan schietgeluid.
Bronniveau van het mondingsgeluid en detonatiegeluid
Het gegevensbestand bevat octaafbandspectra van het bronniveau van mondingsgeluid en detonatiegeluid, voor een aantal richtingen. De spectra zijn geordend als een matrix LEb(Φj,f), voor de octaafbanden met middenfrequenties fk = 16 Hz, 31,5 Hz, ..., 4.000 Hz en N hoeken Φj met j = 1, 2, ..., N. De hoek Φj is hierbij gedefinieerd als de hoek tussen de lijn van bron naar rekenpunt en de vuurlijn (vanuit de bron met de klok mee gemeten, in een bovenaanzicht). De waarde Φ = 0° komt dus overeen met de schietrichting. Als er in het bronnenbestand voor een bepaalde wapen-munitiecombinatie geen bronniveaus opgenomen zijn voor hoeken groter dan 180°, wordt uitgegaan van een symmetrische uitstraling rond de schietrichting. Bronniveaus in richtingen die niet in het gegevensbestand zijn opgenomen worden door interpolatie bepaald.
Als in het gegevensbestand de bronsterkte alleen voor 0° gegeven is, betekent dit dat deze bron richtingsonafhankelijk is. De gegeven bronsterkte geldt dan voor alle hoeken.
In die gevallen waarbij de schietrichting niet bepaald is (bijvoorbeeld op oefenterreinen) wordt de bron als een richtingsonafhankelijke puntbron gemodelleerd. Het richtingsonafhankelijke spectrum wordt uit het hoekafhankelijke bronspectrum bepaald door een gewogen energetische middeling volgens de formule:
| (4.6) |
waarbij wordt verstaan onder:
LEb(fk): het energetisch gemiddelde bronniveau
LEb(fk, Φj): het bronniveau in richting Φj ten opzichte van de schietrichting
N: aantal beschikbare hoeken
gj: gewichtsfactor
De gewichtsfactor wordt bepaald volgens de formule:
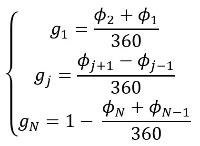
Interpolatiemethode
Met behulp van de matrix LEb(Φj,fk) kan het octaafbandspectrum van het bronniveau voor een willekeurige hoek Φ worden berekend door interpolatie. Hiervoor wordt de zogenaamde cubic spline interpolatiemethode gebruikt. De methode is hieronder beschreven voor een willekeurige octaafband. Er is hierbij uitgegaan van een symmetrische geluidemissie. Voor het gemak is het argument fk in LEb(Φj,fk) weggelaten. Drie gevallen worden onderscheiden:
- •
0.° ≤ Φ < Φ1;
- •
ΦN < Φ ≤ 180°;
- •
Φj < Φ < Φj+1 voor een index j < N.
In de eerste twee gevallen is interpolatie niet mogelijk. De bronsterkte wordt dan bepaald volgens de formules:
| Voor 0° ≤ Φ< Φ1 |
| Voor ΦN< Φ ≤ 180° |
In het derde geval wordt de bronsterkte bepaald volgens de formule:
LEb(ϕ) = ALEb(ϕj) + BLEb(ϕj) + CL''Eb(ϕj + DL''Eb(ϕj+1 | (4.7) |
met
| B = 1 − A |
|
|
L"Eb(Φ)j is de tweede-orde afgeleide van de functie LEb(Φ) voor Φ = Φj. Voor j=1 tot N zijn deze waarden in het gegevensbestand opgenomen.
4.4.2. Gegevensbestand voor bepaling bodemdemping
Het gegevensbestand voor de bepaling van de bodemdemping bevat resultaten van berekeningen met een numeriek rekenmodel voor geluidoverdracht, het Parabolic-Equation model (PE model). Het betreft berekeningen van de bodemdemping voor de 27 meteorologische klassen exclusief geometrische demping en luchtdemping. De berekeningsresultaten zijn gegeven als coëfficiënten van een twintigste-orde polynoom. De bodemdemping voor een specifieke situatie wordt bepaald volgens de formule:
| (4.8) |
waarbij wordt verstaan onder:
ci coëfficiënten van twintigste-orde polynoom;
R horizontale afstand van bronpunt naar rekenpunt.
De 21 coëfficiënten van de polynoom zijn in het bestand gegeven voor:
- •
27 meteorologische klassen;
- •
3 waarden voor de akoestische bodemhardheid (reflecterend, absorberend en zeer absorberend);
- •
12 hoogten van rekenpunten (0,1; 0,5; 1; 1,5; 2; 3; 4; 5; 6; 8; 10 en 15 m);
- •
16 bronhoogten (0,1; 0,5; 1; 1,5; 2; 3; 4; 5; 6; 8; 10; 15; 20; 30; 40 en 50 m);
- •
9 octaafbanden (16 Hz t/m 4.000 Hz).
Totaal bevat dit bestand dus 21×27×3×12×16×9= 2.939.328 coëfficiënten.
Meteorologische klassen
In deze methode worden 27 meteorologische klassen onderscheiden. Een klasse wordt gerepresenteerd door een functie, die de geluidsnelheid beschrijft als functie van de hoogte; het zogenaamde geluidsnelheidsprofiel. Deze profielen zijn in drie groepen onderverdeeld:
groep 1: cn(h) = c10 + bn[(h/h0 + 1)−0.3 − 1] | Voor n = 1 ... 7; |
groep 2: cn(h) = c10 + bnln(h/h0 + 1) | Voor n = 8 ... 18; |
groep 3: cn(h) = c10 + bn[(h/h0 + 1)+0.3 − 1] | Voor n = 19 ... 27. |
(4.9) |
waarbij wordt verstaan onder:
cn(h) geluidsnelheidsprofiel;
h hoogte t.o.v. plaatselijk maaiveld;
h0 referentiehoogte h0= 0,1 m;
c10 geluidsnelheid bij 10° C en 1 atmosfeer (zie paragraaf 2.10);
bn parameter van het geluidsnelheidsprofiel (zie tabel 4.1).
Groep 1 | b1= 10 | b2=3 | b3= 1 | b4= -1 | b5= -3 | b6= -6 | b7= -10 |
Groep 2 | b8= -1 | b9= -0.4 | b10= -0,2 | b11= 0 | b12= 0,2 | b13= 0,4 | b14= 0,7 |
b15= 1,1 | b16=1,5 | b17= 2 | b18= 2,5 | ||||
Groep 3 | b19= -1 | b20= -0,5 | b21= -0,2 | b22= 0,2 | b23= 0,4 | b24= 0,65 | b25= 1 |
b26= 1,4 | b27= 2 |
Formule (4.8) is vanaf 15 m tot een bepaalde maximum afstand geldig. De minimale en maximale afstand zijn in het gegevensbestand opgenomen. Voor afstanden groter dan de maximale afstand wordt de waarde op de maximale afstand genomen. Voor afstanden kleiner dan 15 m kan formule 4.8 niet worden toegepast. Als echter het geluidpad over verschillende bodemtypen loopt kan het voorkomen dat een bronpunt op korte afstand van een bodemovergang ligt en over een afstand kleiner dan 15 m de bodemdemping moet worden bepaald (zie ook paragraaf 4.6.4).
In dat geval moet gebruik worden gemaakt van onderstaande interpolatieformule:
| Voor R < 15m | (4.10) |
Interpolatie en extrapolatie
Het gegevensbestand is gevuld voor een gekozen verzameling van combinaties van hoogtes van het bron- en rekenpunt. Deze verzameling kan worden uitgebreid met de reciproque combinaties. Het reciprociteitsprincipe houdt in dat de waarde van de bodemdemping niet verandert als bron- en rekenpunt worden omgewisseld. In formule:
Dbodem(hs,hr) = Dbodem(hr,hs) | (4.11) |
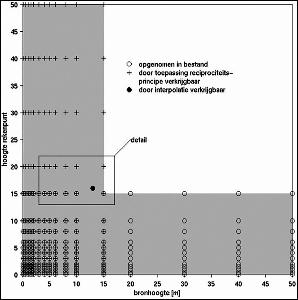
Figuur 4.2a: Overzicht van combinaties van bronhoogte en hoogte van het rekenpunt die in het gegevensbestand zijn opgenomen of die door toepassing van het reciprociteitsprincipe kunnen worden verkregen.
Als een combinatie van bron en rekenpunt binnen het grijs gemarkeerde gebied van figuur 4.2a ligt maar niet in het gegevensbestand voorkomt en ook niet als reciproque combinatie bestaat, zal voor deze combinatie de bodemdemping door interpolatie moeten worden bepaald. Hiervoor worden die vier punten gebruikt, die op de hoekpunten liggen van een rechthoek rond het te interpoleren punt [hs,hr] (zie figuur 4.2.b). De overdracht voor de gewenste combinatie van bronhoogte en hoogte van het rekenpunt wordt vervolgens gegeven volgens de formule:
| (4.12) |
met
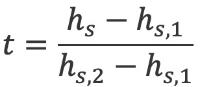
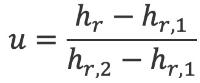
waarbij wordt verstaan onder:
hs hoogte bronpunt boven plaatselijk maaiveld;
hr hoogte rekenpunt boven plaatselijk maaiveld;
hs,k, hr,n hoogte van bronpunt resp. rekenpunt voor (k,n) = (1,1), (1,2), (2,1), en (2,2) waarvan de combinatie wel in het gegevensbestand is opgenomen (zie figuur 4.2b).
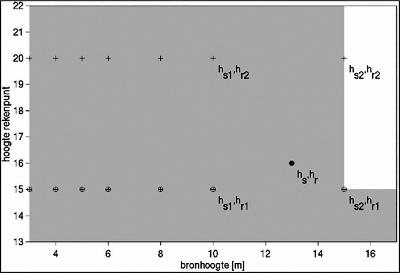
Figuur 4.2b: Detail van figuur 4.2a. Aangegeven is hoe de geluidoverdracht door interpolatie kan worden bepaald.
Als een combinatie niet binnen het grijs gemarkeerde gebied van figuur 4.2a ligt, wordt de bodemdemping door extrapolatie bepaald met behulp van onderstaande relatie:
Dbodem(hs,hr) = Dbodem(15,hs) + Dbodem(15,hr) − Dbodem(15,15) | (4.13) |
Als de hoogte van de bron of van het rekenpunt kleiner is dan 0,1 m moet 0,1 m worden aangehouden. Voor hoogten groter dan 50 m heeft dit gegevensbestand geen geldigheid meer.
4.4.3. Gegevensbestand met statistische gewichten
Een statistisch gewicht geeft de kans aan dat een meteorologische situatie van een klasse m voorkomt. Deze kans hangt van verschillende factoren af. Zo is de kans afhankelijk van het dagdeel (meteorologische dag of meteorologische nacht) respectievelijk aangegeven met het symbool gd(m,θ) en gn(m,θ). De kans is bovendien afhankelijk van de hoek θ die de lijn van bron naar rekenpunt maakt met het geografische noorden en tot slot ook van de gemiddelde bodemruwheid onder het geluidpad (zie ook paragraaf 4.6.7 en paragraaf 4.6.8).
Een maat voor de bodemruwheid is de ruwheidslengte z0. In tabel 4.2 zijn de ruwheidslengtes gegeven waarvoor de statistische gewichten bepaald zijn.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
z0 (cm) | 0,02 | 0,1 | 0,5 | 1,2 | 3 | 6 | 10 | 15 | 20 | 25 |
De gemiddelde ruwheid van de bodem wordt bepaald als gewogen gemiddelde van de ruwheidslengtes van de gebieden langs het geluidpad.
| (4.14) |
waarbij wordt verstaan onder (zie ook figuur 4.3):
z0,j ruwheidslengte van doorlopen deelgebied j;
rmin,j kortste horizontale afstand van bron tot grens deelgebied langs geluidpad;
rmax,j grootste horizontale afstand van bron tot grens deelgebied langs geluidpad;
r horizontale afstand van bron naar rekenpunt langs geluidpad;
N aantal door het geluidpad doorsneden deelgebieden.
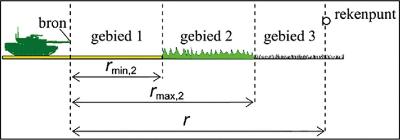
Figuur 4.3: Definitie van grenzen van ruwheidsgebieden bij bepaling van de gemiddelde ruwheid.
In het gegevensbestand statgew.bin zijn voor 10 verschillende waarden van de ruwheid (zie tabel 4.2), voor 60 verschillende hoeken (in stappen van 6°) en voor de 27 meteorologische klassen de statistische gewichten gegeven voor de meteorologische dag en de nacht. Voor waarden van de ruwheid waarvoor in het gegevensbestand geen gewicht is opgenomen wordt het gewicht van de dichtstbijgelegen ruwheidswaarde gebruikt. Voor waarden van de hoek waarvoor geen gewicht is opgenomen wordt een geïnterpoleerde waarde berekend volgens de formule:
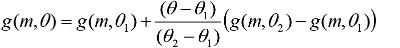
waarin θ1 en θ2 de dichtstbijgelegen hoeken zijn. Dit gegevensbestand bevat hiervoor 27×2×10×60 = 32.400 verschillende statistische gewichten.
In het bovenstaande gegevensbestand hebben een aantal statistische gewichten een waarde gelijk aan nul of relatief een lage waarde (<0,01). De bijdrage voor deze profielen zal gering zijn. Eventueel kunnen deze bijdragen worden toegeschreven aan profiel 18 om zo de berekeningen te vereenvoudigen. Het statistisch gewicht van de profielen met een kleine bijdragen moet dan bij het statisch gewicht van profiel 18 worden opgeteld zodat de som van de gewichten weer gelijk aan 1 is.
Voor het geval dat het gebruik van de schietbaan gekoppeld is aan de heersende windrichting wordt een aangepaste procedure gebruikt. In dit geval is er een zogenaamde windroossector gedefinieerd waarmee een gedeelte van de windroos wordt aangegeven waarbij schietactiviteiten op de schietbaan kunnen plaatsvinden. Deze windroossector wordt door twee parameters bepaald, die de grootte en positie van de sector aangeven (zie paragraaf 2.4 en figuur 4.4). De statistische gewichten zijn van deze twee parameters afhankelijk naast de hiervoor genoemde grootheden (meteorologische klasse, dagdeel, hoek van bron naar rekenpunt met geografisch noorden en de gemiddelde ruwheid onder het geluidpad). Omdat het teveel opslagruimte zou vragen om voor alle mogelijke combinaties van al deze parameters de gewichten te geven is een rekenprocedure ontwikkeld waarmee de gewichten op eenvoudige wijze kunnen worden bepaald.
Voor de berekening wordt gebruik gemaakt van twee gegevensbestanden (statmet.bin en metprof.bin). In het eerste bestand wordt de kans gegeven dat een bepaalde combinatie van windsnelheid, windrichting en bewolkingsgraad voorkomt. Voor de meteorologische dag zijn deze kansen als seizoensgemiddelde gegeven (dus achtereenvolgens voor de lente, zomer, herfst en de winter), voor de meteorologische nacht wordt een jaargemiddelde waarde gebruikt. Met het tweede bestand kan worden bepaald bij welke omstandigheden welke meteorologische klasse hoort.
Het is een groot bestand waarin de meteorologische klasse gegeven wordt als functie van:
- •
gemiddelde ruwheid onder het geluidpad (voor 10 ruwheden zie tabel 4.2);
- •
geluidvoortplantingsrichting (voor 0° tot 354° in stappen van 6°);
- •
windsnelheid (voor 15 klassen);
- •
windrichting (voor 0° tot 354° in stappen van 6°);
- •
bewolkingsgraad (voor 9 klassen);
- •
seizoen (voor de meteorologische dag voor 4 seizoenen; voor de meteorologische nacht is een jaargemiddelde gegeven).
De berekening van een statistisch gewicht verloopt dan als volgt: eerst wordt bepaald welke gedigitaliseerde waarden van de windrichting (lopend van 0° tot 354° in stappen van 6°) binnen de windroossector liggen. Vervolgens wordt de dichtstbijgelegen ruwheidswaarde uit tabel 4.2 gekozen, die overeenkomt met de gemiddelde ruwheidswaarde onder het geluidpad (zie formule 4.14). Voor deze waarden wordt in bestand metprof.bin gezocht naar alle combinaties van windsnelheid, windrichting, bewolkingsgraad en — voor de meteorologische dag — seizoen, die bij een van de 27 meteorologische klassen horen. Met behulp van het bestand statmet kan de kans worden bepaald dat een dergelijke combinatie optreedt. Per meteorologische klasse worden de kansen gesommeerd van al de combinaties, die bij die klasse horen. Uit de zo verkregen waarden (27 voor de meteorologische dag en 27 voor de meteorologische nacht) worden tenslotte de statistische gewichten bepaald door deze 27 waarden te normeren met hun som voor respectievelijk de dag en de nacht zodat geldt:
| (4.15) |
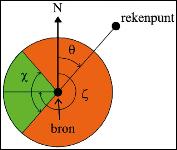
Figuur 4.4: Een windroossector [χ, ζ] betekent dat alleen windrichtingen ζ ± χ/2 relevant zijn (de groene sector in de figuur). Dit voorbeeld toont een windroossector [90°, 270°], waarbij alleen windrichtingen tussen noordwest en zuidwest relevant zijn. De hoek θ, die de lijn van bron- naar rekenpunt maakt met het geografische noorden, is ook aangegeven.
Als de geluidvoortplantingsrichting niet gelijk is aan een veelvoud van 6° tussen 0° en 354° dan wordt bovenstaande procedure uitgevoerd voor de twee dichtstbijgelegen waarden voor de richting. Het uiteindelijk gewicht wordt vervolgens (vergelijkbaar met hoe dit hiervoor is aangegeven) door lineaire interpolatie bepaald.
4.5. Invoergrootheden rekenmethode
4.5.1. Brongegevens
Mondingsgeluid
Voor de berekening van de geluidbelasting van het mondingsgeluid moeten van elke wapen-munitiecombinatie de volgende geometrische parameters bekend zijn:
- •
(xs,ys, hwapen) wapenpositie, waarbij hwapen de hoogte van het wapen is ten opzichte van het plaatselijke maaiveld;
- •
αe elevatie van wapen;
- •
ψ schietrichting t.o.v. het noorden in het horizontale vlak.
De bronnen van het mondingsgeluid worden gerepresenteerd als puntbronnen. De positie van de puntbron ligt voor lichte wapens aan het uiteinde van de loop, voor zwaardere wapens ligt dit punt op enige afstand van de vuurmond in het verlengde van de loop. In het gegevensbestand van bronnen is hiermee rekening gehouden door de looplengte te definiëren als de afstand van het draaipunt tot aan het bronpunt. De bronpositie kan zo met behulp van eenvoudige geometrische formules uit bovenstaande gegevens worden berekend (zie formule 4.4).
Militaire oefenterreinen
Bij militaire oefenterreinen zijn de exacte bronposities vaak onbekend. Wel kan een gebied worden aangegeven waar mogelijk geschoten wordt. Voor de modellering van een oefenterrein worden daarom gebieden geselecteerd waarbinnen kan worden aangenomen dat de kans dat op een mogelijke positie geschoten wordt uniform over dit gebied verdeeld is en waarbij elke schietrichting even waarschijnlijk is. Er is hierbij vanuit gegaan dat alleen met losse patronen wordt geschoten. Als niet aan deze voorwaarden wordt voldaan, zal van de exacte bronpositie uit moeten worden gegaan.
Voor de modellering van een oefenterrein verdient het aanbeveling van een referentie-oefening uit te gaan. De volgende benaderingen zijn daarbij gebruikelijk om de geluidbelasting door schieten en knallen te beschrijven:
- 1.
Er wordt een referentieoefening gedefinieerd. Deze bestaat uit diverse oefensituaties die aan een gebied worden gekoppeld. Bijvoorbeeld: ‘Patrouille zuivert bosgebied in dagperiode’.
- 2.
Het aantal knallen per munitiesoort en wapentype wordt uniform verdeeld gedacht over de diverse gebieden waarin deze oefening voorkomt, tenzij uitdrukkelijk anders aangegeven.
- 3.
Als niet uitdrukkelijk anders wordt aangegeven, wordt uitgegaan van de energetisch gemiddelde bronsterkte per wapentype over alle (horizontale) richtingen (zie formule 4.6). In het bijzonder geldt dit voor gevallen waarin een aanvallende en verdedigende partij is.
- 4.
In paragraaf 4.6.1 is aangegeven hoe de gebieden moeten worden opgedeeld voor de overdrachtsberekening.
- 5.
Omdat er met losse patronen of simulatoren wordt geoefend, speelt kogelgeluid geen rol.
Kogelgeluid
Uit het bronnenbestand kan worden gelezen of voor een wapen-munitiecombinatie de startsnelheid van het te verschieten projectiel supersoon is. In dit geval kan kogelgeluid van belang zijn. Voor lichte wapentypen wordt er voor de berekening vanuit gegaan dat de kogelbaan evenwijdig aan de bodem loopt. De elevatie is voor deze wapentypen dus 0°.
Kogelgeluid van de zwaardere wapentypen waarvan het projectiel een kromme baan beschrijft (het zogenaamde krombaangeschut; Houwitser en mortier) moet op een andere wijze worden berekend. Voor de berekening van het kogelgeluid moet dan rekening worden gehouden met de sterk variërende hoogte van de kogel.
Voor banen waarbij gebruik wordt gemaakt van een vervangende puntbron, zie hieronder, wordt de bijdrage van zowel mondingsgeluid als kogelgeluid verdisconteerd. Kogelgeluid wordt dan niet apart berekend.
Bij hagelgeweren wordt eventueel kogelgeluid verdisconteerd in de bronsterkte van het mondingsgeluid.
Detonatiegeluid
Ook het detonatiegeluid wordt in de rekenmethode als een puntbron gekarakteriseerd. De hoogte van deze puntbron is afhankelijk van de hoogte van detonatie. Bij een brisantgranaat is het moment (en dus de hoogte) van detonatie afhankelijk van het type ontstekingsbuis dat op een granaat is aangebracht. Dit kan variëren van 10 m hoogte tot in de grond. Als de detonatie in of op de grond plaatsvindt, wordt voor de berekening een hoogte van 0,5 m+ maaiveld aangehouden.
Schietbanen (zoals bijvoorbeeld schermenschietbanen)
In die gevallen waarbij het wapen op korte afstand deels of geheel omsloten is door afschermende of reflecterende objecten, kan in principe niet van brongegevens worden uitgegaan, die voor het vrije veld zijn bepaald. Het geluidveld rond de bron is dermate complex dat het gebruik van rekenmodellen, die vanaf de bron rekenen, beperkt mogelijk is. Voor deze gevallen wordt de situatie van de bron met de omringende afschermende of reflecterende objecten gemodelleerd door één of meer vervangende puntbronnen. De bronsterkte van deze vervangende puntbron(nen) zal met metingen moeten worden vastgesteld. In de Toelichting op toepassing van methoden voor meten en rekenen aan schietgeluid wordt een beschrijving van de meetmethode gegeven. Als geen meetgegevens voorhanden zijn of te verkrijgen zijn, wordt in dit rapport ook een conservatieve inschatting gegeven voor een vervangende puntbron op basis van de vrije-veld bronsterkte. In sommige gevallen kan het gewenst zijn dat de bronsterkte van deze schietbanen met berekeningen wordt vastgesteld, bijvoorbeeld voor nog niet bestaande schietbanen. Per situatie moet een rekenmodel op zijn geschiktheid worden beoordeeld, een algemeen toepasbaar model is vooralsnog niet te geven.
Voor de modellering van een schietbaan (zoals bijvoorbeeld een kleiduivenschietbaan) verdient het aanbeveling van een standaard gebruikssituatie uit te gaan. In het eerder genoemde rapport (TNO 2014 R10135) wordt voor een aantal type banen aangegeven hoe deze moeten worden gemodelleerd om de geluidbelasting te berekenen.
4.5.2. Bodemtype (hardheid/ruwheid)
In het model worden vier verschillende bodemtypen onderscheiden (zie tabel 4.3). Elk type correspondeert met een andere combinatie van bodemhardheid en bodemruwheid (zie voor definities van deze begrippen paragraaf 2.5)
Bodemtype | Voorbeelden | σ (Nsm−4) | zo (m) |
|---|---|---|---|
1. glad en reflecterend | water, beton | ∞ | 0,0002 |
2. ruw en absorberend | grasland | 3·105 | 0,03 |
3. ruw en zeer absorberend | zandbodem | 1·105 | 0,03 |
4. zeer ruw en zeer absorberend | heide, bouwland | 1·105 | 0,25 |
Om het bodemtype van een terrein te bepalen moeten eerst de eigenschappen van terrein worden ingeschat. De volgende uitgangspunten moeten hierbij in acht worden genomen:
- 1.
De keuze tussen ruw en zeer ruw.
Het verschil tussen ruw en zeer ruw zit in de begroeiing van de oppervlakte.
Een ruw terrein bevat lage begroeiing (zoals gras), een zeer ruw terrein bevat hogere begroeiing (zoals heide of lage gewassen). Verspreide obstakels (bomen, huizen) worden hierbij buiten beschouwing gelaten.
- 2.
De keuze tussen absorberend en zeer absorberend.
Een bodem wordt absorberend genoemd als de stromingsweerstand groter is dan 2·105 Nsm−4, en zeer absorberend als de stromingsweerstand kleiner is dan 2·105 Nsm−4. Dit betekent in de praktijk dat grasland absorberend is en dat ruwere bodems zoals heide zeer absorberend zijn.
- 3.
Voor bossen en steden moet bodemtype 4 worden gekozen.
Als in het overdrachtspad van bron naar rekenpunt verschillende bodemtypen voorkomen, moeten ze ook zo worden onderscheiden. In paragraaf 4.6.4 wordt hier nader op ingegaan.
4.5.3. Afschermende objecten
Een object moet aan de volgende eisen voldoen om als afschermend object in rekening te worden gebracht:
- •
De massa per eenheid van oppervlakte bedraagt ten minste 10 kg/m2.
- •
Het object mag geen grote kieren of openingen bevatten. Procesinstallaties, bomen e.d. worden dus niet als een afschermend object in rekening gebracht.
- •
Het object wordt vanuit de bron of vanuit het rekenpunt gezien onder een hoek van ten minste 5° in het horizontale vlak.
Grote objecten, zoals heuvels en eventueel duinen waarbij het terrein een hellingspercentage kent van minder dan 20%, worden niet als afschermende objecten ingevoerd. Deze kunnen in rekening gebracht worden door een variatie in de maaiveldhoogte van de bodemvlakken.
Drie verschillende afschermende objecten worden onderscheiden:
- •
scherm;
- •
wal;
- •
gebouw.
Een scherm en een wal worden geschematiseerd door een verticaal vlak of keten van verticale vlakken, die onder een hoek met elkaar staan, waarbij er vanuit wordt gegaan dat de bovenrand horizontaal loopt. Bij een wal wordt de positie van het vlak op het snijpunt gekozen van het voor- en achtervlak van de wal. Voor de berekening moet de hoogte bekend zijn, voor een wal moet bovendien de tophoek worden opgegeven. De definitie van de tophoek is in onderstaande figuren gegeven. Als een scherm op een wal zo laag is dat de gestippelde lijnen in figuur 4.5b het talud snijden, wordt de grootte van de tophoek bepaald zoals dit in figuur 4.5a is weergegeven.
|
|
Figuur 4.5a: Tophoek γ van wal met platte top. | Figuur 4.5b: Tophoek γ van wal met scherm |
Bij een wal is de absorptiecoëfficiënt van het materiaal waaruit het is opgebouwd van belang voor de berekening van de tophoekcorrectie (formule 4.50). Enkele typerende waarden van de absorptiecoëfficiënt zijn voor verschillende materialen in tabel 4.4 aangegeven.
Gebouwen worden geschematiseerd als een keten van verticale vlakken van dezelfde hoogte, waarbij het eerste vlak weer aan het laatste vlak aansluit. Er wordt verondersteld dat de hoogte van al deze vlakken gelijk is.
4.5.4. Reflecterende objecten
Er worden twee typen reflecties onderscheiden: spiegelreflecties en diffuse reflecties. Voor een spiegelreflectie geldt dat de hoek van inval van het geluid gelijk is aan de hoek die het gereflecteerde geluid maakt met het spiegelende object, vergelijkbaar met een optische spiegeling. Bij diffuse reflecties wordt het invallende geluid diffuus verstrooid.
Spiegelende objecten
Twee verschillende spiegelende objecten worden onderscheiden:
- •
scherm;
- •
gebouw.
Een object moet aan de volgende eisen voldoen om als spiegelend reflecterend object in rekening te worden gebracht:
- •
Het object heeft een min of meer vlakke en geluidreflecterende wand;
- •
De reflecterende wand moet een dichtheid hebben groter dan 10 kg/m2;
- •
De hoek tussen de geluidreflecterende wand en de verticaal moet kleiner zijn dan 10°.
De spiegelende objecten worden op dezelfde manier geschematiseerd als de overeenkomstige afschermende objecten. Van een reflecterend vlak moet daarnaast ook de reflectiviteit (0 ≥ ρ ≥ 1) worden gegeven. De reflectiviteit ρ is de reflectiecoëfficiënt voor de geluidenergie en wordt bepaald door de absorptiecoëfficiënt αabs van het materiaal waaruit het reflecterende vlak bestaat:
ρ = 1-αabs. In het algemeen is ρ een functie van de frequentie. Enkele typerende waarden van de absorptiecoëfficiënt zijn voor verschillende materialen in tabel 4.4 aangegeven.
Materiaal | Geluidabsorptiecoëfficiënt, in octaafbanden | ||||||||
|---|---|---|---|---|---|---|---|---|---|
16 | 31.5 | 63 | 125 | 250 | 500 | 1.000 | 2000 | 4.000 | |
Bakstenen muur | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,1 | 0,1 |
Dichte betonblokken (pleister, verf) | 0,0 | 0,0 | 0,1 | 0,1 | 0,1 | 0,.1 | 0,1 | 0,1 | 0,1 |
Poreuze betonblokken | 0,0 | 0,1 | 0,2 | 0,4 | 0,4 | 0,3 | 0,3 | 0,4 | 0,3 |
Glazen wand | 0,1 | 0,2 | 0,3 | 0,4 | 0,3 | 0,2 | 0,1 | 0,1 | 0,0 |
Houten wand | 0,0 | 0,1 | 0,2 | 0,3 | 0,2 | 0,2 | 0,1 | 0,1 | 0,1 |
Aarde en zand, glad | 0,0 | 0,0 | 0,0 | 0,1 | 0,1 | 0,1 | 0,2 | 0,4 | 0,5 |
Aarde, ruw | 0,0 | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,6 | 0,6 | 0,6 |
Grind, los en vochtig, (laag van 10cm) | 0,0 | 0,1 | 0,2 | 0,3 | 0,6 | 0,7 | 0,7 | 0,8 | 0,8 |
Gras | 0,0 | 0,0 | 0,1 | 0,1 | 0,2 | 0,3 | 0,4 | 0,6 | 0,7 |
Diffuus reflecterende objecten
Diffuse reflecties treden op aan een bosrand; als er minder dan drie bomenrijen aanwezig zijn, wordt de diffuse reflectie niet meegerekend. Een diffuse reflectie treedt op als er `zicht' is op de bosrand vanuit zowel de positie van de bron als de positie van het rekenpunt; optische spiegeling is hierbij irrelevant. Een bosrand wordt gemodelleerd door een verticaal vlak of keten van verticale vlakken, die onder een hoek met elkaar staan, waarbij er vanuit wordt gegaan dat de bovenrand horizontaal loopt. Op de plaats van de vlakken wordt één rij van equidistante cilinders gedacht. De afstand tussen de cilinders deff bedraagt de helft van de gemiddelde afstand tussen naburige bomen van de eerste drie bomenrijen van de bosrand. Deze gemiddelde afstand wordt benaderd door 1/√n2, waarbij n2 het gemiddelde aantal bomen per oppervlakte-eenheid is. De straal van de cilinders rcil is gelijk aan de gemiddelde straal van de bomen in de bosrand. Indicatieve waarden voor een gemiddeld bos zijn deff = 1,4 m en rcil = 0,1 m. De hoogte van de bosrand wordt bepaald door de gemiddelde hoogte van de bomen in de bosrand.
4.5.5. Keuze van rekenpunten
Voor planningsdoeleinden zijn vaak contouren gewenst. Een geluidcontour is een lijn die punten met een gelijke geluidbelasting verbindt. Een geluidcontour kan worden verkregen door lineaire interpolatie tussen rekenpunten op een rekenrooster. Een rekenrooster is een verzameling van punten, die op regelmatige afstand (d*) van elkaar liggen. Aan de interpolatie zijn een aantal voorwaarden verbonden:
- •
het verschil in geluidniveau tussen de punten bedraagt minder dan 3 dB;
- •
de afstand tussen het geïnterpoleerde punt en het dichtstbijzijnde bronpunt is groter dan de afstand tussen de punten waartussen wordt geïnterpoleerd.
In de meeste gevallen zal bij een afstand van d* = 250 m aan bovenstaande criteria worden voldaan. Als niet aan bovenstaande voorwaarden wordt voldaan, zal het rooster lokaal verdicht moeten worden. Een verdere verdichting dan tot d* = 50 m is niet noodzakelijk.
Hoogte rekenpunt
Als er sprake is van zonering rondom schietbanen of -terreinen, heeft een hoogte van 5 m de voorkeur. Voor beoordelingspunten bij vergunningsituaties wordt over het algemeen voor de dagperiode een hoogte van 1,5 m en voor de avond- en nachtperiode een hoogte van 5 m aangehouden. Uitgangspunt is dat de berekeningshoogte bepaald wordt door de hoogte waarop mogelijke hinder te verwachten is.
4.6. Berekening van het geluidexpositieniveau
4.6.1. Bronniveau
Mondingsgeluid en detonatiegeluid
Voor geluid anders dan kogelgeluid wordt het bronniveau over het algemeen betrokken uit het gegevensbestand. Zie hiervoor paragraaf 4.4.1 en paragraaf 4.5.1. De emissie van het mondingsgeluid is over het algemeen richtingsafhankelijk. Van belang hierbij is de hoek Φ tussen de vuurlijn en de lijn van bron naar rekenpunt. Deze hoek is afhankelijk van de elevatie αevan het wapen volgens de formule:
Φ = acos(cosαe cosΦp)
waarbij wordt verstaan onder:
Φp hoek tussen de lijn van bron naar rekenpunt en de vuurlijn (in bovenaanzicht vanuit de bron met de klok mee gemeten) geprojecteerd op een horizontaal vlak.
Bij de berekening van de emissiehoek Φ wordt geen rekening gehouden met hoogteverschillen tussen bronpunt en rekenpunt (benadering voor het verre veld).
Brongebieden
Brongebieden zijn gebieden waarbinnen een mogelijke schietpositie uniform over het gebied is verdeeld. Om de geluidbelasting van een brongebied te berekenen, moet dit in zodanig kleine deelgebieden worden opgedeeld dat voor een deelgebied van een puntbron kan worden uitgegaan.
In een eerste stap wordt, afhankelijk van de kleinste en grootste afstand van het rekenpunt tot de grenzen van het brongebied (respectievelijk dmin en dmax), de breedte bepaald van schillen die in concentrische cirkels rond het rekenpunt liggen. Voor de breedte Ln van deze schillen geldt:
| (4.16) |
voor n = 1 t/m N
waarin N, uitgedrukt als een naar boven afgerond geheel getal, wordt bepaald volgens de formule:
| (4.17) |
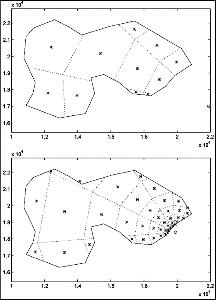
Figuur 4.6: Voorbeeld van een beschrijving van een deelgebied door deelbronnen voor twee verschillende rekenpunten (o).
Vervolgens worden deze schillen onderverdeeld in sectoren met een hoek van 30°. De snijpunten van de concentrische cirkels met de sector begrenzingen geven de hoekpunten van trapezia. De overlap van deze trapezia met het brongebied geven uiteindelijk de grenzen van de verschillende deelgebieden. De vervangende deelbronnen liggen op het geometrische zwaartepunt van deze deelgebieden.
In figuur 4.6 is een voorbeeld gegeven van de verdeling van de bronpunten voor twee verschillende rekenpunten.
De bijdragen van de verschillende deelbronnen tot de geluidbelasting in de verschillende juridische beoordelingsperioden (Bs,dag(bi), Bs,avond(bi) en Bs,nacht(bi)) moeten tenslotte worden gecorrigeerd voor het verschil in oppervlak tussen de verschillende deeloppervlakken Oi en het totale oppervlak van het brongebied Otot. Hiertoe wordt in formule 3.4 in het rechterlid een correctieterm toegevoegd volgens de formule:
| (4.18) |
| |
|
Kogelgeluid bij vlakbaan schieten
Voor de berekening van de geluidbelasting door kogelgeluid wordt ervan uitgegaan dat het kogelgeluid van één punt afkomt dat op de kogelbaan ligt, het zogenaamde bronpunt. Uitgaande van een xy-coördinatenstelsel in het horizontale vlak, met de vuurmond in de oorsprong, de x-as langs de vuurlijn en de y-as loodrecht hierop, wordt de positie van het bronpunt aangegeven als (xs,0) en de positie van het rekenpunt als (xr,yr). De onbekende xs wordt bepaald door het oplossen van onderstaande vierde orde polynoom:
(xr − xs)2 (v0 + v1xs + c10) (v0 + v1xs − c10) = c102 yr2 met 0 ≤ xs < xr en xs <| (c10 − v0) / v1| | (4.19) |
waarbij wordt verstaan onder:
(xr,yr) positie van rekenpunt;
(xs,0) positie van het bronpunt.
Voor de oplossing van deze polynoom wordt verwezen naar mathematische handboeken. Als het bronpunt achter het doel ligt, wordt voor het bronpunt de doelpositie genomen. Als het bronpunt op een punt ligt waar de kogelsnelheid kleiner is dan 1,02c0 dan wordt voor het bronpunt het punt genomen waar de kogelsnelheid gelijk is aan 1,02c0 (ervan uitgaande dat v0 groter is dan 1,02c0).
Het breedbandige bronniveau wordt bepaald door de afmetingen van de kogel en zijn lokale snelheid op het bronpunt:
| (4.20) |
met M het Mach-getal van de kogel op het bronpunt en waarbij dkogel en lkogel worden uitgedrukt in m.
Voor de berekening van het octaafbandspectrum van het bronniveau wordt rekening gehouden met de verschuiving van het spectrum van kogelgeluid op het traject van het bronpunt naar het rekenpunt (door niet-lineaire effecten). Hiervoor wordt een karakteristieke frequentie fkogel van kogelgeluid geïntroduceerd, die afhankelijk is van de afstand R van het bronpunt op de kogelbaan naar het rekenpunt:
| (4.21) |
Omdat het tertsbandspectrum wordt gebruikt bij de berekening van de luchtdemping (zie paragraaf 4.6.3) wordt het bronniveau in tertsen bepaald. Hierbij wordt uitgegaan van de drie tertsbanden binnen de octaven met middenfrequenties fk van 16 Hz tot en met 4 kHz. Het bronspectrum in tertsen wordt bepaald volgens de formule:
| Voor k = 1..9 en j = 1..3 | (4.22) |
waarin:

met:
fk,j nominale middenfrequentie van je tertsband van ke octaafband
Voor de berekeningen van de overige dempingstermen wordt van een bronspectrum in octaven uitgegaan:
| (4.23) |
Kogelgeluid bij krombaan schieten
In het algemeen is het kogelgeluid bij krombaan schieten niet van belang. Door de hoge elevatiehoek waaronder geschoten wordt en de verhoudingsgewijs lage uittreesnelheid van het projectiel in vergelijking tot lichte vuurwapens, treedt kogelgeluid alleen in een klein gebied voor het wapen op. Dit gebied ligt dus in het mal onveilige gebied (mog) van het wapen en is daarom voor de berekening van de geluidbelasting in woongebieden niet van belang.
Echter, in speciale gevallen waarbij de elevatiehoek lager ligt en de uittreesnelheid verhoudingsgewijs groot is, is het kogelgeluid wel van belang. In deze gevallen moet voor de berekening van de geluidbelasting door kogelgeluid een daarvoor geschikte methode worden gebruikt.
4.6.2. Geometrische demping
Puntbronnen
Bij de modellering van puntbronnen is uitgegaan van sferische geluiduitbreiding over een hele bol. De geometrische demping wordt bepaald volgens de formule:
| (4.24) |
Kogelgeluid
Voor de berekening van de geometrische demping van kogelgeluid worden drie gebieden onderscheiden (zie figuur 2.2): gebied I achter het wapen, gebied II dat ook als Mach-gebied wordt aangeduid, en gebied III achter het doel. De grenzen tussen de gebieden worden bepaald door de hoeken ξb en ξe, die afhankelijk zijn van de beginsnelheid v0 respectievelijk de eindsnelheid ve van de kogel (ve is dus de kogelsnelheid bij het treffen van het doel):
| (4.25) |
Als de snelheid van de kogel voor het treffen van het doel onder de geluidsnelheid is gezakt geldt ξe = 0, in dit geval bestaat er dan geen gebied III.
In het gebied achter het wapen (gebied I) is het kogelgeluid verwaarloosbaar.
Voor rekenpunten in gebied II varieert de geometrische demping tussen 10 lg R en 25 lg R afhankelijk van de afstand R van het bronpunt op de kogelbaan tot het rekenpunt. De geometrische demping is 10 lg R op korte afstand van de kogelbaan bij een constante kogelsnelheid. Als gevolg van een afname van de snelheid van de kogel langs de kogelbaan en door invloed van turbulentie neemt de geometrische demping toe. De invloed van turbulentie is pas op een afstand Rtrans van de kogelbaan significant. Op grote afstand, groter dan 10 km, bedraagt de geometrische demping 20 lg R.
De transitieafstand Rtrans wordt bepaald met de formule:
| (4.26) |
met
xt lengte van de kogelbaan waar het projectiel een supersone snelheid heeft
L correlatielengte (L = 1.1 m)
μ02 = 10−5
De geometrische demping in gebied II wordt voor R ≤ Rtrans bepaald volgens de formule:
| (4.27a) |
voor Rtrans < R ≤ Rmax geldt:
| (4.27b) |
voor R >Rmax geldt:
| (4.27c) |
met
k = -v1/c10
r0 = 1 m
Rmax = 10 km
Vóór het wapen maar buiten het Mach-gebied (gebied III) wordt de geometrische demping door twee termen bepaald:
- •
de geometrische demping berekend volgens formule 4.27 voor het traject R1van de doelpositie naar een punt op de grens van het Mach-gebied dat het dichtst bij het rekenpunt ligt (punt P in figuur 4.7);
- •
een extra demping die afhankelijk is van de afstand (R2) van dit punt P tot aan het rekenpunt:
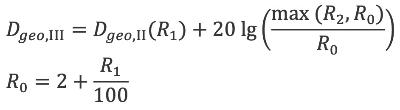
(4.28)
waarbij wordt verstaan onder:
R1 de afstand van de doelpositie naar een punt op de grens van het Mach-gebied dat het dichtst bij het rekenpunt ligt;
R2 de afstand van het rekenpunt tot de grens van het Mach-gebied.
De afstanden R1 en R2 worden alleen voor de berekening van de geometrische demping in gebied III gebruikt, voor het berekenen van de overige dempingstermen wordt van het geluidpad uitgegaan van het bronpunt op de kogelbaan (in dit geval dus de doelpositie) naar het rekenpunt.
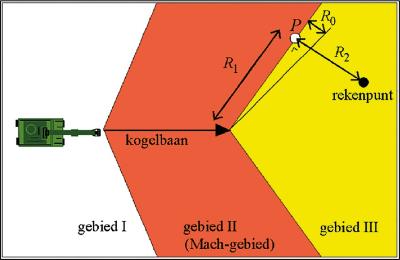
Figuur 4.7: Definitie van R1, R2 en R0 uit formule 4.28.
4.6.3. Luchtdemping
Bij de berekening van de luchtdemping wordt rekening gehouden met de vorm van het spectrum. Per octaafband (index k) wordt geschat hoe de geluidenergie over de drie tertsbanden (index j) binnen dit octaaf verdeeld is. Deze geluidenergie kLEb,j(f) wordt bepaald op basis van een lineaire interpolatie van de niveaus van de naburige octaafbanden (bij kogelgeluid is dit niet nodig daar kogelgeluid per tertsband wordt berekend zie ook paragraaf 4.6.1):
| (4.29) |
met:
LEb(f0) = 2LEb(f1) − LEB(f2)
LEb(f10) = 2LEb(f9) − LEB(f8)
waarbij wordt verstaan onder:
LEb,j(fk) het bronniveau van de je tertsband (j = 1 t/m 3) van de octaafband met centrumfrequentie fk (k = 1 t/m 9).
De luchtdemping in de ke octaafband Dlucht(fk) wordt vervolgens bepaald uit het gewogen energetische gemiddelde van de luchtdemping van de tertsbanden binnen deze octaafband.
| (4.30) |
De waarden voor de luchtdemping αlu,j(fk) in tertsband j = 1, 2 en 3 van de ke octaafband zijn ontleend aan ISO-norm 9613-1 voor 10°C en 80% relatieve vochtigheid. Deze waarden zijn (in dB per km) opgenomen in tabel 4.5.
Nummer van tertsband binnen octaaf | Octaafbandmiddenfrequentie in Hz | ||||||||
|---|---|---|---|---|---|---|---|---|---|
16 | 31.5 | 63 | 125 | 250 | 500 | 1.000 | 2.000 | 4.000 | |
j=1 | 0,00452 | 0,0179 | 0,0669 | 0,254 | 0,764 | 1,63 | 2,86 | 6,23 | 19,0 |
j=2 | 0,00715 | 0,0282 | 0,108 | 0,378 | 1,02 | 1,97 | 3,57 | 8,76 | 28,7 |
j=3 | 0,0113 | 0,0444 | 0,167 | 0,547 | 1,31 | 2,36 | 4,62 | 12,7 | 43,9 |
4.6.4. Bodemdemping
In paragraaf 4.4.2 is omschreven hoe de bodemdemping met behulp van het gegevensbestand moet worden bepaald. In deze paragraaf wordt beschreven hoe de bodemdemping moet worden bepaald als er verschillende bodemvlakken door het geluidpad worden doorsneden, welke invloed de turbulentie heeft op de bodemdemping en hoe de bodemdemping moet worden bepaald als er in het geluidpad afschermende obstakels zijn.
De bodemdemping is afhankelijk van:
- •
de horizontale afstand R tussen de bron (of spiegelbron) en rekenpunt;
- •
de akoestische bodemhardheid (aangegeven met index ν). In de methode worden drie bodemhardheden onderscheiden (zie paragraaf 4.5.2): v=z voor een zeer absorberende bodem, v=a voor een absorberende bodem en v=h voor een harde bodem;
- •
de frequentie;
- •
de hoogtes van bron- en rekenpunt;
- •
de meteorologische klasse.
In deze paragraaf geven we alleen de eerste twee parameters expliciet aan als argumenten van Dbodem:
| (4.31) |
met ck(ν) de coëfficiënten van het polynoom.
Meer dan een bodemvlak
Als onder het geluidpad bodemtypen liggen met verschillende bodemhardheid worden voor mee- en tegenwindsituaties verschillende procedures toegepast.
- •
Meewindsituaties (profielnrs. 4 t/m 7, 12 t/m 18 en 22 t/m 27)
Om de bodemdemping voor meer dan een bodemvlak te bepalen, worden voor de meewindsituaties eerst de horizontale afstanden (sv) bepaald, waarover het geluidpad door de verschillende bodemgebieden loopt. Voor elke bodemhardheid worden deze afstanden opgeteld.
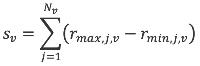
(4.32)
waarbij wordt verstaan onder:
Nv aantal gebieden dat door het geluidpad wordt doorkruist met respectievelijk een zeer absorberende (v=z), een absorberende (v=a) en een harde bodem (v=h);
rmin,j,v , rmax,j,v minimale en maximale horizontale afstand van bron tot de grens van deelgebied j gemeten langs het geluidpad voor een bodemgebied met hardheid v (zie hierboven).
De bodemdemping voor een meewindsituatie wordt vervolgens bepaald door de formule:
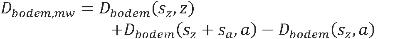
(4.33)
- •
Tegenwindsituaties (profielnrs. 1 t/m 3, 8 t/m 10 en 19 t/m 21)
Voor de bodemdemping bij tegenwindsituaties zijn alleen de bodemgebieden binnen een afstand ds van de bron en binnen een afstand dr van het rekenpunt van belang. Deze afstanden zijn afhankelijk van het profiel, van de frequentie en van de hoogte boven het plaatselijk maaiveld van respectievelijk bron- en rekenpunt.
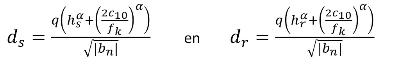
(4. 34)
met:
q = 21, 10, 16,5 en α = 0,9, 0,85, 0,78 voor respectievelijk de groepen 1, 2 en 3 van de geluidsnelheidsprofielen (zie formule 4.9). Ook parameter bn wordt bepaald door het profiel (zie tabel 4.1 in § 4.4.2).
De gebieden mogen elkaar niet overlappen. Als ds + dr>R, waarin R de horizontale afstand tussen bron en rekenpunt is, moeten de afstanden in verhouding worden teruggeschaald tot ds' en dr'.
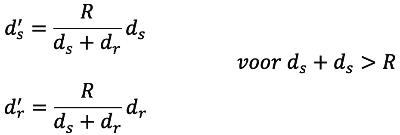
(4.35)
Binnen een afstand ds en dr van respectievelijk bron en rekenpunt worden achtereenvolgens de afstanden bepaald waarover het geluidpad door zeer absorberende, absorberende en reflecterende gebieden loopt. In verhouding tot de afstand ds + dr geeft dit de fracties fz, fa en fh zeer absorberende, absorberende en reflecterende bodem. De bodemdemping voor een tegenwindsituatie wordt vervolgens berekend volgens de formule:
Dbodem,tw(r) = fzDbodem(r, z) + faDbodem(r, a) + fhDbodem(r, h)
(4.36)
- •
Neutraal profiel (profielnr. 11)
Voor de bepaling van de bodemdemping van de neutrale situatie (profielnr. 11) worden eerst de fracties fz, fa en fh bepaald over de totale afstand rtot tussen bron en rekenpunt. De bodemdemping volgt dan door toepassing van formule 4.36.
Turbulentie
De totale bodemdemping is naar boven toe begrensd als gevolg van turbulentie. Deze begrenzing is afhankelijk van de meteorologische klasse, de hardheid van de bodem en de frequentie. Bij het berekenen van de overdrachtsfuncties zoals deze in het gegevensbestand zijn opgenomen is dit effect niet verdisconteerd. Deze invloed wordt in rekening gebracht door een bovengrens Dbodem,max te stellen aan de bodemdemping zoals die met formule 4.37 bepaald is. In situaties met afschermende objecten moet de bovengrens worden toegepast op de som Dbodem + Dscherm.
In tabel 4.6 zijn de grenswaarden van de bodemdemping gegeven voor de verschillende bodemhardheden, de 27 meteorologische klassen en de 9 octaafbanden.
m | v | 16 | 31.5 | 63 | 125 | 250 | 500 | 1.000 | 2.000 | 4.000 |
|---|---|---|---|---|---|---|---|---|---|---|
z | 25 | 26 | 20 | 17 | 19 | 20 | 24 | 25 | 26 | |
1 | a | 25 | 26 | 19 | 15 | 18 | 20 | 24 | 25 | 26 |
h | 25 | 25 | 17 | 9 | 13 | 17 | 22 | 24 | 26 | |
z | 29 | 18 | 22 | 21 | 22 | 19 | 18 | 19 | 20 | |
2 | a | 29 | 18 | 21 | 19 | 21 | 19 | 18 | 19 | 20 |
h | 29 | 17 | 19 | 13 | 16 | 16 | 16 | 18 | 20 | |
z | 29 | 29 | 17 | 24 | 25 | 19 | 17 | 18 | 19 | |
3 | a | 29 | 29 | 16 | 22 | 24 | 19 | 17 | 18 | 19 |
h | 29 | 29 | 14 | 16 | 19 | 16 | 15 | 17 | 19 | |
z | 26 | 26 | 17 | 14 | 18 | 22 | 26 | 27 | 28 | |
8 | a | 26 | 26 | 16 | 12 | 17 | 22 | 26 | 27 | 28 |
h | 26 | 25 | 14 | 6 | 12 | 19 | 24 | 26 | 28 | |
z | 24 | 23 | 20 | 16 | 18 | 19 | 21 | 22 | 23 | |
9 | a | 24 | 23 | 19 | 14 | 17 | 19 | 21 | 22 | 23 |
h | 24 | 22 | 17 | 8 | 12 | 16 | 19 | 21 | 23 | |
z | 29 | 19 | 22 | 20 | 21 | 18 | 18 | 19 | 20 | |
10 | a | 29 | 19 | 21 | 18 | 20 | 18 | 18 | 19 | 20 |
h | 29 | 18 | 19 | 12 | 15 | 15 | 16 | 18 | 20 | |
z | 29 | 29 | 19 | 23 | 27 | 19 | 19 | 20 | 21 | |
11 | a | 29 | 29 | 18 | 21 | 26 | 19 | 19 | 20 | 21 |
h | 29 | 29 | 16 | 15 | 21 | 16 | 17 | 19 | 21 | |
z | 28 | 25 | 14 | 16 | 21 | 24 | 29 | 29 | 29 | |
19 | a | 28 | 25 | 13 | 14 | 20 | 24 | 29 | 29 | 29 |
h | 28 | 24 | 11 | 8 | 15 | 21 | 27 | 29 | 29 | |
z | 26 | 26 | 16 | 14 | 19 | 21 | 25 | 26 | 27 | |
20 | a | 26 | 26 | 15 | 12 | 18 | 21 | 25 | 26 | 27 |
h | 26 | 25 | 13 | 6 | 13 | 18 | 23 | 25 | 27 | |
z | 23 | 23 | 18 | 15 | 18 | 19 | 20 | 21 | 22 | |
21 | a | 23 | 23 | 17 | 13 | 17 | 19 | 20 | 21 | 22 |
h | 23 | 22 | 15 | 7 | 12 | 16 | 18 | 20 | 22 | |
z | 29 | 29 | 22 | 24 | 27 | 24 | 29 | 29 | 29 | |
Overig | a | 29 | 29 | 21 | 22 | 26 | 24 | 29 | 29 | 29 |
h | 29 | 29 | 19 | 16 | 21 | 21 | 27 | 29 | 29 |
Als onder het geluidpad verschillende bodemtypen liggen met verschillende bodemhardheid, wordt de bovengrens Dbodem,max berekend volgens de formule:
Dbodem,max = fzDbodem,max(z) + faDbodem,max(a) + fhDbodem,max(h) | (4.37) |
met:
Dbodem,max(v) bovengrens voor bodemtype v voor een bepaald profiel.
De fracties fz, fa en fh worden voor de meewindprofielen en het neutrale profiel bepaald over de totale afstand tussen bron en rekenpunt, voor de tegenwindprofielen worden de fracties bepaald over een gereduceerd gebied bij bron- en rekenpunt, zoals dit boven formule 4.36 is beschreven. De begrenzing wordt toegepast nadat met formule 4.33 c.q. 4.36 de bodemdemping berekend is en de eventuele schermwerking bepaald is.
Effectieve hoogte van bron of rekenpunt
Bij de bepaling van de bodemdemping is ook de hoogte van bron- en rekenpunt van belang. Als het geluidpad één scherm snijdt dan wordt de hoogte van één van beide vervangen door een effectieve hoogte, afhankelijk van welk punt het dichtst bij het scherm staat. Als meer dan een scherm doorsneden wordt, worden de effectieve hoogtes van zowel het bron- als rekenpunt gebruikt. Eerst worden de schermen daarvoor in twee groepen verdeeld; schermen die dichter bij de bron staan dan bij het rekenpunt en schermen die dichter bij het rekenpunt staan dan bij de bron. De effectieve hoogte voor de bron wordt bepaald op basis van het meest effectieve scherm uit de eerste groep, de effectieve hoogte voor het rekenpunt wordt bepaald op basis van het meest effectieve scherm uit de tweede groep (zie formule 4.53 in paragraaf 4.6.5). Als geen schermen in een groep vallen, wordt voor de effectieve hoogte de werkelijke hoogte van de bron of het rekenpunt genomen.
4.6.5. Afscherming
In situaties waarin het verticale vlak door het bron- en rekenpunt een object snijdt (bijvoorbeeld een geluidscherm), wordt de invloed van dit object in formule 4.2 in rekening worden gebracht door de term Dscherm. In andere situaties is deze term gelijk aan nul.
Situaties met één scherm
Een scherm wordt geschematiseerd door een verticaal staande rechthoek. Drie geluidpaden worden onderscheiden. Eén pad via de top van het scherm en twee paden via de zijkanten van het scherm (zie figuur 4.8). De verticale schermhoogte zsch,1 is de hoogte van het scherm ten opzichte van het laagste aan het scherm grenzende maaiveld. De ‘horizontale schermhoogten’ zsch,2 en zsch,3 zijn in figuur 4.9 gedefinieerd.
|
|
Figuur 4.8: Geluid bereikt het rekenpunt achter een eindig scherm via de top en via de zijkanten van een scherm. | Figuur 4.9: Definitie van ‘horizontale schermhoogten’ in een bovenaanzicht van een scherm tussen bron en rekenpunt. |
Afhankelijk van de meteorologische situatie zijn de geluidpaden meer of minder gekromd. Hiermee wordt rekening gehouden bij de bepaling van de schermwerking. De schermwerking wordt daarom per meteorologische klasse bepaald.
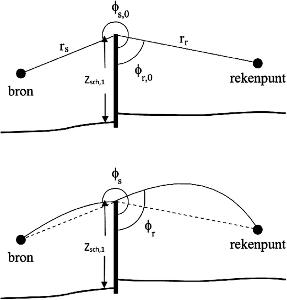
Figuur 4.10: Straalkromming
De straalkromming wordt in rekening gebracht door correcties ΔΦs en ΔΦ toe te passen op de hoeken Φs,0 en Φr,0 die in figuur 4.10 zijn aangegeven (alle hoeken in deze paragraaf worden in radialen uitgedrukt). In formule:
ϕs = ϕs,0 − Δϕs ϕr = ϕr,0 − Δϕr | (4.38) |
Er wordt alleen rekening gehouden met straalkromming voor de zogenaamde meewindprofielen (n = 4 t/m 7, 12 t/m 18, 22 t/m 27 in tabel 4.1). Voor de andere profielen geldt ΔΦs = 0 en ΔΦr = 0. Ook voor de geluidpaden 2 en 3 (de horizontale omwegen) in figuur 4.9 wordt straalkromming buiten beschouwing gelaten. In de overige gevallen zijn deze correcties te bepalen uit de maximale hoogte van de geluidstraal zmax,n.
Voor de berekening van zmax,n wordt eerst voor elk meewindprofiel een hoogte zmax0,n berekend volgens de formule:
| voor n = 4 ... 7 | (4.39) |
| voor n = 12 ... 18 | (4.40) |
| voor n = 22 ... 27 | (4.41) |
waarin:
| (4.42) |
met:
fk octaafbandmiddenfrequentie (f6 = 500 Hz);
fabs fractie van het geluidpad waarvoor de bodem ‘absorberend’ of ‘zeer absorberend’ is;
Δx de horizontale afstand (langs het geluidpad) van bron- of rekenpunt naar het scherm afhankelijk of ΔΦs dan wel ΔΦr moet worden bepaald;
bn parameter van het geluidsnelheidsprofiel (zie tabel 4.1).
Voor zmax,n geldt nu:
| (4.43) |
De correcties zijn vervolgens te bepalen volgens de onderstaande formule (t = s of r, zie ook formule 4.9):
| (4.44) |
De demping door het scherm wordt per geluidpad (p=1,2,3) berekend volgens de formule:
Dscherm,p = max(0; Hp ·[10 lg(arg) − ∆Dp]) | (4.45) |
met
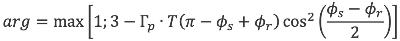
Opmerking: Φs en Φr zijn beide een functie van zowel de frequentie, het meteorologisch profiel als het geluidpad.
In bovenstaande formule worden de volgende functies toegepast:
max(x;y) is gelijk aan de grootste van zijn twee argumenten:
| (4.46) |
T(x) geeft het teken van x aan:
| (4.47) |
Γp is gedefinieerd als:
| (4.48) |
waarbij wordt verstaan onder:
rs afstand van bron naar top van scherm (zie figuur 4.10);
rr afstand van rekenpunt naar top van scherm.
De factor Hp brengt de eindige afmetingen van het scherm in rekening volgens de formule:
| (4.49) |
ΔDp is de tophoekcorrectie voor een wal met tophoek γ (zie figuur 4.5). Deze correctie wordt alleen toegepast voor geluidpad 1 over de top van het obstakel:
| (4.50) |
ΔD2,3 = 0
waarbij wordt verstaan onder:
ρ = 1 − αabs
δ = max(0;min(0,3; Φs − Φr − π))
αabs de frequentieafhankelijke absorptiecoëfficiënt van de zijvlakken van de wal (0 ≤ αabs ≤ 1). Voor een harde wal geldt αabs = 0, voor een zachte wal geldt αabs = 1, bij speciale gevallen kan hiervan worden afgeweken).
Φs, Φr diffractiehoeken voor geluidpad 1.
Voor de tophoek γ geldt de restrictie 0,25π ≤ γ ≤ 0,9π. Voor een wal met γ > 0,9π moet de waarde γ = 0,9π worden gebruikt. Voor een wig met γ < 0,25π geldt ΔD = 0.
De totale schermwerking Dscherm wordt berekend uit de schermwerkingen Dscherm,p van de drie geluidpaden, volgens de formule:
| (4.51) |
Bovenstaande formule geldt voor het neutrale profiel (profielnr. 11) en de tegenwindsituaties (profielnrs. 1 t/m 3, 8 t/m 10 en 19 t/m 21). Bij alle meewindsituaties (profielnrs. 4 t/m 7, 12 t/m 18 en 22 t/m 27) geldt formule 4.51 alleen voor de octaafbandmiddenfrequenties van 16 Hz tot 250 Hz. Boven 250 Hz geldt bij alle meewindsituaties:
Dscherm(fn) = Dscherm(f5) | voor | fn ≥ f5 = 250 Hz | (4.52) |
Een schermdemping groter dan 20 dB is over het algemeen moeilijk te realiseren. Als de berekende schermdemping voor een octaafband groter is dan 20 dB moet men er alert op zijn dat door omloopgeluid (bijvoorbeeld door een diffuse reflectie aan een bijliggend object) of door de aanwezigheid van turbulente wervels in de atmosfeer de effectieve werking van het scherm deels kan worden tenietgedaan. Daarom wordt de schermdemping begrensd op 20 dB, tenzij nader onderzoek aantoont dat hogere reducties kunnen worden bereikt.
Meervoudig scherm
Als een aantal schermen aan elkaar vastzit, dan spreken we van een meervoudig scherm. Alleen concave meervoudige schermen worden in beschouwing genomen. Een voorbeeld van een concaaf meervoudig scherm is weergegeven in figuur 4.11.
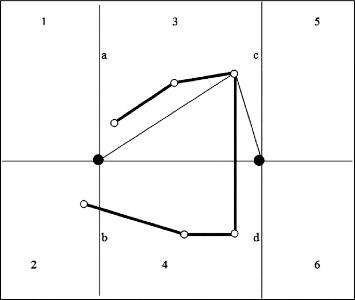
Figuur 4.11: Meervoudig scherm met zes hoekpunten. De linker omweg is aangegeven. Er is geen rechter omweg mogelijk in deze situatie. Lijn a—b gaat in dit horizontale vlak door het bronpunt en lijn c—d door het rekenpunt.
De schermwerking wordt als volgt berekend:
- 1.
Pad via top van het scherm:
Eerst wordt bepaald welke schermen worden gesneden door het verticale vlak door bron- en rekenpunt. Vervolgens wordt het scherm geselecteerd waarbij het verschil tussen de diffractiehoeken Φs,0 − Φr,0 het grootst is. Als geen enkel scherm gesneden wordt is Dscherm = 0.
- 2.
Pad via de zijkanten van het scherm:
Het horizontale vlak wordt verdeeld in zes gebieden, gescheiden door een lijn door rekenpunt en bronpunt en door twee lijnen a-b en c-d, die hier dwars opstaan (zie figuur 4.11).
- a)
Linker omweg. Bepaal het snijpunt van de lijn van bronpunt naar rekenpunt met het in stap 1 geselecteerde scherm. Volg het meervoudige scherm naar links. Als het meervoudige scherm lijn a of lijn c snijdt, wordt de linker omweg niet meegerekend. De Hp(fk) is dan gelijk aan 1 (zie formule 4.49 en 4.51) en Dscherm,p = ∞. Als het meervoudige scherm lijn a en lijn c niet snijdt, wordt van alle hoekpunten in gebied 3 het hoekpunt geselecteerd met de grootste waarde van het horizontaal diffractiehoek-verschil Φs — Φr. Dit hoekpunt bepaalt de linker omweg.
- b)
Rechter omweg: analoog.
De procedure is ook van toepassing op een gesloten meervoudig scherm, waarbij beginpunt en eindpunt van het scherm samenvallen. Een voorbeeld hiervan is een gebouw.
Meer dan een scherm
In situaties met meer dan een scherm tussen bron- en rekenpunt worden maximaal twee schermen in rekening gebracht. Eerst worden de schermen in twee groepen verdeeld: een groep met schermen die zich dichter bij de bron bevinden en een groep met schermen die zich dichter bij het rekenpunt bevinden. Van beide groepen wordt het scherm geselecteerd met het grootste verschil van de diffractiehoeken (Φs,0 — Φr,0) voor de verticale omweg. De schermwerkingen van de twee geselecteerde schermen worden, inclusief de bijdragen van de horizontale omwegen, bij elkaar opgeteld. Deze som geeft de totale schermwerking.
De effectieve bronhoogte (van toepassing bij de bepaling van de bodemdemping) wordt bepaald op basis van het geselecteerde scherm uit de eerste groep, de effectieve hoogte van het rekenpunt wordt bepaald op basis van het geselecteerde scherm uit de tweede groep.
Effectieve hoogte van bron- of rekenpunt
Bij de bepaling van de bodemdemping wordt, als het geluidpad een scherm snijdt, de hoogte van het bronpunt of van het rekenpunt (afhankelijk van het feit of het bronpunt of het rekenpunt dichter bij het scherm ligt) vervangen door een effectieve hoogte:
| (4.53) |
waarbij wordt verstaan onder:
Φs, Φr diffractiehoeken voor geluidpad 1.
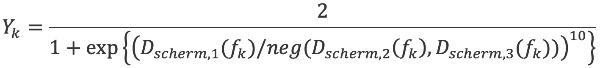
met
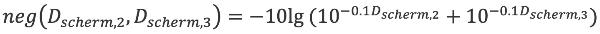
Bovenstaande formule is gegeven voor het bepalen van de effectieve hoogte van de bron. Voor de bepaling van de effectieve hoogte van het rekenpunt moet hs worden vervangen door hr.
Bij de berekening van de bodemdemping bij reflecties wordt — als sprake is van afscherming- voor de bepaling van de effectieve hoogte uitgegaan van het geluidpad van gespiegelde bron naar rekenpunt. Het reflecterend vlak heeft hierbij geen invloed op de bepaling van de effectieve hoogte.
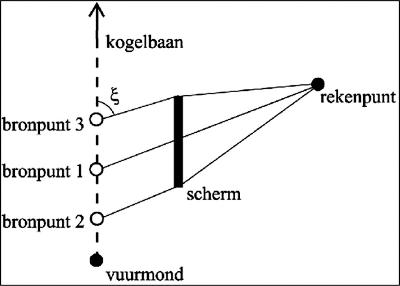
Figuur 4.12: Schematische weergave van afscherming van kogelgeluid.
Afscherming kogelgeluid
Voor de afscherming van kogelgeluid wordt in principe dezelfde benadering gevolgd als bij afscherming voor mondingsgeluid of detonatiegeluid. Ook hierbij worden drie geluidpaden onderscheiden: een pad over de top van het obstakel en twee paden langs de zijkanten van het scherm. Het verschil is echter dat deze drie geluidpaden over het algemeen verschillende bronpunten op de kogelbaan hebben (zie figuur 4.12). Het bronpunt van het pad over de top is gelijk aan het bronpunt voor de onafgeschermde situatie; de twee andere bronpunten worden bepaald door formule 4.19 met (Xr, Yr) respectievelijk de linker en rechter zijkant van het scherm. Als kogelgeluid is afgeschermd, wordt de bijdrage van het kogelgeluid bepaald uit de energetisch gesommeerde bijdragen van de drie bronnen die op deze drie bronposities gedacht kunnen worden. Dit betekent dat per bron alle dempingstermen (geometrische-, lucht-, bodem-, niet-lineaire en schermdemping) moeten worden bepaald.
Figuur 4.13: Berekening van kogelgeluidbijdrage voor situaties waarbij het mondingsgeluid is afgeschermd maar een rand van het scherm in het Mach-gebied ligt.
Er is sprake van afscherming als de lijn van het bronpunt van het kogelgeluid (bepaald in de niet afgeschermde situatie) naar het rekenpunt het scherm snijdt, anders is er sprake van een onafgeschermde situatie en wordt de systematiek gehanteerd, die hiervoor beschreven is. Een uitzondering hierop is de situatie die in nevenstaande figuur is afgebeeld waarbij het rekenpunt in gebied I ligt en het mondingsgeluid wordt afgeschermd. Eén verticale rand van het scherm ligt echter in het Mach-gebied (gebied II). Ook in deze situatie wordt een kogelgeluidbijdrage berekend. Hierbij wordt er maar één (horizontaal) geluidpad beschouwd en wel langs de verticale rand van het scherm dat in het kogelgeluidgebied ligt. Deze bijdrage wordt echter alleen meegenomen als de bovenrand van het scherm ten minste 1 m boven de mond van het wapen uitsteekt.
De bronsterkten van de genoemde drie bronnen (of één bron voor het laatst genoemde geval) worden bepaald zoals in paragraaf 4.6.1 beschreven. De geometrische demping wordt op dezelfde manier bepaald als voor onafgeschermd kogelgeluid conform de formules die in § 4.6.2. voor kogelgeluid zijn beschreven. Het is hierbij van belang in welk gebied een verticale rand van een scherm ligt (zie figuur 4.7). Als bijvoorbeeld een schermrand in gebied III ligt moet voor de geometrische demping formule 4.28 worden toegepast. Over het algemeen is dus de geometrische demping voor de verschillende combinaties verschillend aangezien de bronposities niet gelijk hoeven te zijn. Ook de lucht-, bodem- en niet-lineaire demping worden (vergelijkbaar met de berekeningsmethode voor afgeschermd mondingsgeluid) bepaald voor het directe pad van bronpunt naar rekenpunt. De schermdemping tot slot wordt bepaald met formule 4.45 waarbij per bronpunt maar één pad wordt beschouwd overeenkomend met het pad dat in figuur 4.12 staat aangegeven. De tophoekcorrectie wordt alleen toegepast voor het pad over de top van het obstakel. Voor de situatie die in figuur 4.13 is weergegeven wordt dus geen tophoekcorrectie toegepast. Verder zijn dezelfde restricties van toepassing als die bij formule 4.50 en 4.52 zijn gegeven.
Voor het bepalen van de geluidbelasting (zie formule 3.1 t/m 3.7 in hoofdstuk 3) worden eerst de verschillende bijdragen van het afgeschermde kogelgeluid — langs maximaal drie verschillende paden — energetisch gesommeerd.
4.6.6. Niet-lineaire demping
Alleen voor de berekening van de geluidbelasting door kogelgeluid wordt een dempingsterm in rekening gebracht, die voortkomt uit de niet-lineaire overdracht van kogelgeluid. Deze term is alleen van toepassing voor rekenpunten in gebied II. Hiervoor geldt de formule:
| (4.54) |
met
r0 = 1 m
k = -v1 / c10
Voor rekenpunten in gebied III wordt deze term alleen over de afstand R1 in rekening gebracht.
4.6.7. Spiegelreflecties
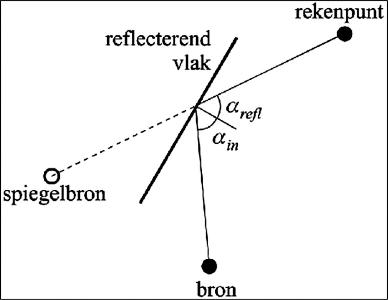
Figuur 4.14: Voor een spiegelreflectie geldt dat de hoek van inval (αin) gelijk is aan de hoek van reflectie (αrefl). Een spiegelreflectie wordt gemodelleerd met behulp van een spiegelbron.
Spiegelreflecties aan objecten worden in rekening gebracht door gebruik te maken van spiegelbronnen. Hierbij moet aan een aantal eisen worden voldaan (zie paragraaf 4.5.4):
- 1.
Het object heeft een min of meer vlakke en geluidreflecterende wand.
- 2.
De reflecterende wand moet een dichtheid hebben groter dan 10 kg/m2. Bomenrijen en open procesinstallaties worden zo buitengesloten.
- 3.
Het geluid moet via een reflectie (zoals bij optische spiegeling) het rekenpunt kunnen bereiken. De hoek tussen de geluidreflecterende wand en de verticaal moet daarom kleiner zijn dan 10°. Van een talud kan dus geen reflectiebijdrage komen.
Als een object meer dan een reflectievlak heeft (zoals een scherm met enige hoeken), moet ieder vlak van het object als een mogelijk afzonderlijk reflecterend object worden beschouwd.
Op het geluidpad tussen bron- en rekenpunt worden alleen enkelvoudige reflecties in de berekening meegenomen.
Het bronniveau van een spiegelbron L*Eb is lager dan het bronniveau van de originele bron; L*Eb wordt bepaald uit bronniveau LEb van de originele bron volgens de formule:
L*Eb = LEb − Drefl | (4.55) |
waarin LEb het bronniveau (per octaafband) van de originele bron in de richting van het reflectiepunt is en Drefl de reflectiedemping. De reflectiedemping voor spiegelreflecties wordt bepaald volgens de formule:
Drefl = −10lg(εhor εverρ) | (4.56) |
waarbij wordt verstaan onder:
εhor de ‘horizontale’ reflectie-effectiviteit (0 ≤ εhor ≤ 1),
εver de ‘verticale’ reflectie-effectiviteit (0 ≤ εver ≤ 1),
ρ de reflectiviteit (0 ≤ ρ ≤ 1).
De reflectiviteit ρ wordt bepaald door de absorberende eigenschappen van het materiaal waaruit het reflecterende vlak bestaat. In het algemeen is ρ een functie van de frequentie. Voor een hard vlak geldt ρ = 1.
De horizontale effectiviteit εhor en de verticale effectiviteit εver representeren de invloed van de eindige breedte respectievelijk hoogte van het vlak.
De ‘horizontale’ reflectie-effectiviteit wordt bepaald volgens de formule
| (4.57) |
waarbij wordt verstaan onder:
W1, W2 horizontale afstand van reflectiepunt tot rand reflecterend vlak loodrecht op lijn van bron naar reflectiepunt (zie figuur 4.15);
rb horizontale afstand van de bron tot het reflectiepunt;
λ = c10/fk golflengte die overeenkomt met de octaafbandmiddenfrequentie fk;
αhor = 4,5 een constante.
De horizontale afstand rb van de bron tot het reflectiepunt wordt hierbij kleiner verondersteld dan de afstand van het rekenpunt tot het reflectiepunt; als dit niet zo is dan wordt voor rb de afstand van het rekenpunt tot het reflectiepunt gebruikt.
De afstanden W1 en W2 worden gegeven door de formules W1 = L1 cosα en W2 = L2 cosα, waarin L1 en L2 de afstanden zijn van het reflectiepunt tot de beide randen van het vlak, en α de reflectiehoek is (zie figuur 4.15).
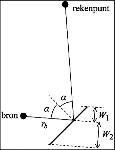
Figuur 4.15: Illustratie van een spiegelreflectie, met daarin aangegeven de afstanden W1 en W2, de horizontale afstand rb van de bron tot het reflectiepunt, en de reflectiehoek α.
De ‘verticale’ reflectie-effectiviteit wordt bepaald volgens de formule
| (4.58) |
waarin Dscherm de schermwerking is van het reflecterende vlak voor de overdracht van de spiegelbron naar het rekenpunt (zie figuur 4.14). De schermwerking is afhankelijk van de geometrie, de frequentie, de meteorologische klasse en het bodemtype. Bij de berekening van Dscherm wordt alleen het geluidpad via de top van het scherm meegerekend; het scherm wordt in horizontale richting dus oneindig lang verondersteld. Er wordt geen tophoekcorrectie toegepast.
Voor de berekening van de geluidoverdracht langs een gereflecteerde straal moet dezelfde procedure worden gevolgd als voor de directe geluidoverdracht, waarbij het verloop van bodemruwheid en bodemhardheid bepaald wordt langs het gereflecteerde geluidpad.
Schermwerking langs dit gereflecteerde geluidpad wordt berekend voor die schermen die door dit pad worden doorsneden. Voor schermen tussen bron en reflecterend object wordt voor de schermwerking uitgegaan van bron en gespiegeld rekenpunt. Voor schermen tussen rekenpunt en reflecterend object wordt voor de schermwerking uitgegaan van de gespiegelde bron en het rekenpunt.
De richting van het geluidpad, aangegeven door hoek θ(b) in formule 3.2 en 3.3, verandert na een reflectie. Voor de berekening van de deelbijdrage tot de geluidbelasting wordt in de genoemde formules echter van de richting van het langste deel van het geluidpad uitgegaan (voor de vaststelling van de hoekafhankelijke bronsterkte wordt natuurlijk uitgegaan van het eerste deel van het geluidpad vanaf de bron).
Reflectie van kogelgeluid
Een reflectie van kogelgeluid kan het rekenpunt alleen bereiken als het rekenpunt zich binnen het gebied bevindt dat door spiegeling van het kogelgeluid wordt bestreken. Dit is geïllustreerd in figuur 4.16.
Uit de positie van het gespiegelde rekenpunt kan het bronpunt op de kogelbaan van het gereflecteerde kogelgeluid worden bepaald. Als het gespiegelde rekenpunt in gebied III ligt wordt de reflectiebijdrage verwaarloosd.
Voor de bepaling van de transitieafstand (zie formule 4.26) wordt voor xt bij de berekening van de reflectiebijdrage dat deel van de kogelbaan genomen waarop bronpunten liggen waarvan het geluid kan reflecteren in het scherm (zie figuur 4.16). Alleen het gedeelte van het scherm dat in gebied II ligt wordt hierbij verdisconteerd.
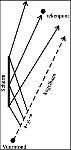
Figuur 4.16: Schematische weergave van de reflectie van kogelgeluid.
4.6.8. Diffuse reflectie
Diffuse reflecties treden op aan een bosrand; als er minder dan drie bomenrijen aanwezig zijn wordt de diffuse reflectie niet meegerekend. Een diffuse reflectie treedt op als er ‘zicht’ is op de bosrand vanuit zowel de positie van de bron als de positie van het rekenpunt; optische spiegeling is hierbij irrelevant. De bijdrage van diffuse reflecties is alleen relevant als het rechtstreekse geluidpad van bron naar rekenpunt wordt afgeschermd. Als deze afscherming voor de 250 Hz octaafband meer dan 8 dB bedraagt (berekend voor profiel 14 mbv formule 4.51) en aan de hiervoor genoemde voorwaarden voldaan wordt, moet diffuus geluid in rekening worden gebracht.
Een bosrand wordt gemodelleerd met één enkele rij van equidistante cilinders (zie figuur 4.17). De afstand tussen de cilinders deff bedraagt de helft van de gemiddelde afstand tussen naburige bomen van de eerste drie bomenrijen van de bosrand. Deze gemiddelde afstand wordt benaderd door
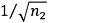
, waarbij n2 het gemiddeld aantal bomen per oppervlakte-eenheid is. De straal van de cilinders rcil is gelijk aan de gemiddelde straal van de bomen in de bosrand. Indicatieve waarden voor een gemiddeld bos zijn deff = 1,4 m en rcil = 0,1 m.
Alle cilinders dragen bij aan de diffuse reflectie. Diffuse reflecties worden gemodelleerd met behulp van virtuele bronnen (zie figuur 4.18a). In principe kan voor elke cilinder een virtuele bron worden gebruikt, maar voor een efficiënte berekening worden de cilinders gegroepeerd in segmenten (zie figuur 4.18b). De lengtes van de segmenten worden zo gekozen dat de hoek waaronder elk segment vanuit de bron gezien wordt ongeveer 5° is (of vanuit het rekenpunt, als dit zich dichter bij de bosrand bevindt). Het aantal cilinders binnen een segment is geheeltallig. De hoek waaronder een segment gezien wordt kan hierdoor enigszins variëren. De precieze grootte van een hoeksector wordt bepaald door het maximaal aantal cilinders dat net binnen een sector van 5° past. Als de hoek waaronder de totale rij cilinders wordt gezien minder dan 5° is, wordt alleen één segment gebruikt. De bijdragen van de virtuele bronnen aan de reflectie kunnen als incoherent worden beschouwd, zodat elke virtuele bron als een aparte bron kan worden behandeld.
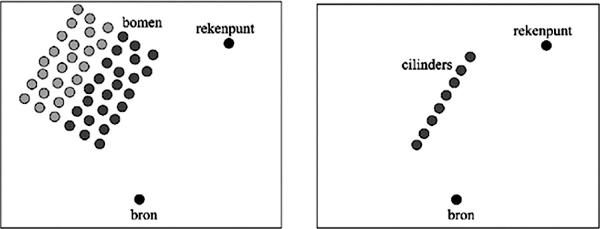
Figuur 4.17: Bij een diffuse reflectie aan een bosrand wordt de bosrand (links) vervangen door één rij equidistante cilinders aan de bosrand (rechts).
|
|
Figuur 4.18a: De bijdrage van een cilinder aan een diffuse reflectie wordt gerepresenteerd door een virtuele bron. Een virtuele bron ligt in het verlengde van de lijn van de cilinder naar het rekenpunt. De afstand van de virtuele bron naar de cilinder is gelijk aan de afstand van de echte bron naar de cilinder. | Figuur 4.18b: Voor een efficiënte berekening worden de cilinders gegroepeerd in segmenten. De bijdragen van de cilinders binnen een segment worden aan elkaar gelijk gesteld, zodat per segment alleen een berekening voor de centrale cilinder hoeft te worden uitgevoerd. |
Net als bij spiegelreflecties wordt door een reflectiedemping Drefl rekening gehouden met het feit dat een virtuele bron zwakker is dan de echte bron. Het bronniveau L*Eb van een virtuele bron (per octaafband) wordt bepaald met formule 4.55. De reflectiedemping Drefl voor diffuse reflecties wordt hierin bepaald volgens de formule:
Drefl = −10lg(εver ρNcil) | (4.59) |
waarbij wordt verstaan onder:
εver ‘verticale’ reflectie-effectiviteit (0 ≤ εver ≤ 1),
ρ reflectiviteit per cilinder (0 ≤ ρ ≤ 1),
Ncil aantal cilinders in het segment.
De verticale reflectie-effectiviteit εver wordt op dezelfde manier berekend als voor spiegelreflecties (zie formule 4.58), waarbij voor de schermhoogte de gemiddelde hoogte van de bomen wordt gebruikt.
De reflectiviteit per cilinder ρ wordt bepaald volgens de formule:
| (4.60) |
met
| (4.61) |
en
| (4.62) |
waarin c1 = 25 m/s, r1 = 25 m en α1 = 10 constanten zijn, en r0 en δΦ parameters die in figuur 4.18b aangegeven zijn; de index n van het segment is hier voor het gemak weggelaten. De parameter δΦ is de hoek tussen de lijnen van de centrale cilinder van het segment naar de bron en naar het rekenpunt.
De parameter r0 is de afstand van de bron tot de centrale cilinder van het segment, waarbij de afstand van de bron tot de centrale cilinder kleiner wordt verondersteld dan de afstand van het rekenpunt tot de cilinder; als dit niet zo is dan moet voor r0 de afstand van het rekenpunt naar de centrale cilinder worden gebruikt.
Bij de overdracht van een virtuele bron naar het rekenpunt treden de dempingen Dgeo, Dlucht, Dbodem en eventueel Dscherm op. De berekening van deze dempingen gaat op dezelfde manier als dit bij spiegelreflecties is beschreven.
5. Beschrijving invoergegevens
5.1. Schietbaan
Over het gebruik van de schietbaan moeten de volgende gegevens worden vermeld:
- •
aantal dagen (07.00 – 19.00 uur), avonden (19.00 – 23.00 uur) en nachten (23.00 – 07.00 uur) per jaar dat de schietbanen in gebruik zijn;
- •
mogelijke beperkingen die gesteld zijn aan het gebruik van de schietbaan;
- •
schietbaantype (zie § 2.7);
- •
akoestische voorzieningen;
- •
lengte van de schietbanen;
- •
locatie van de schietposities;
- •
locatie van de doelposities;
- •
specificatie van de wapentypes en de munitie (met bijbehorende aandrijvende lading) waarmee geschoten wordt;
- •
hoogte van het bronpunt van elk wapentype boven het plaatselijk maaiveld;
- •
aantal schoten per jaar, uitgesplitst naar:
- ○
beoordelingsperiode (dag: 07.00 – 19.00 uur, avond: 19.00 – 23.00 uur, nacht: 23.00 – 07.00 uur), alleen voor de dagperiode wordt dit uitgesplitst naar zon- en feestdagen en overige dagen;
- ○
schietbaan;
- ○
schietpositie;
- ○
doelpositie;
- ○
wapen-munitiecombinatie;
- •
verdeling van de schoten naar de stand waaruit geschoten wordt (liggend of staand).
5.2. Rekenmodel
In het akoestisch rapport moet worden aangetoond dat de situatie valt binnen het toepassingsbereik van deze bijlage.
De volgende gegevens over de gebruikte software moeten worden vermeld:
- •
datum of versie van toegepaste rekenprogramma('s);
- •
datum of versie van de toegepaste gegevensbestanden.
In het rapport moet worden vermeld welke keuzes er zijn gemaakt over de modellering en waarom deze keuzes zijn gemaakt. Wanneer in de modellering wordt afgeweken van deze rekenmethode, moet dit gemotiveerd worden aangegeven.
Als de brongegevens niet in het gegevensbestand zijn opgenomen maar uit emissiemetingen zijn verkregen, moeten deze metingen zijn uitgevoerd zoals beschreven in de Toelichting op toepassing van methoden voor meten en rekenen aan schietgeluid. De beschrijving van de emissiemetingen moet als bijlage aan het rapport worden toegevoegd. Ook kan worden volstaan met een verwijzing naar een bestaande rapportage.
Als de brongegevens niet direct uit metingen zijn bepaald, moet de reden hiervan worden opgegeven en moet worden vermeld hoe deze brongegevens zijn verkregen. Dit moet ook gebeuren als gebruik gemaakt is van de categorie-indeling voor wapen-munitiecombinaties van hand- en vuistvuurwapens. De procedure hiervoor staat beschreven in het eerder genoemde TNO-rapport.
In de hoofdtekst van het akoestisch rapport moet een globale beschrijving van de invoergegevens voor het rekenmodel worden gegeven. Een gedetailleerde beschrijving van de invoergegevens en een grafische weergave van de geometrische invoergegevens wordt als bijlage in het rapport opgenomen.
5.3. Berekeningsresultaten
Voor elk rekenpunt moet voor de drie beoordelingsperioden de geluidbelasting worden gegeven (Bs,dag, Bs,avond en Bs,nacht) samen met de daaruit afgeleide dag-avond-nachtwaarde (Bs,dan) van de geluidbelasting. In de bijlage van het rapport moet de geluidbelasting per bron worden gegeven voor elk rekenpunt en voor elke beoordelingsperiode.
6. Methode voor de berekening van LEs,periode bij een geluidbelasting kleiner dan 50 dB(A)
Hieronder wordt de methode voor de berekening van de deelbijdrage aan de geluidbelasting (LEs,periode, zie formule 3.1) gegeven die kan worden toegepast bij de berekening van geluidniveaus kleiner dan 50 dB. De impulstoeslag (Pimp=12 dB) en de toeslag voor extra laagfrequente componenten in het geluid (Plf(b,m)) worden dan bij de berekening van de geluidbelasting, alleen meegenomen voor zover het geluid waarneembaar is op het immissiepunt. De deelbijdrage LEs,periode(b,m) (zie formule 3.1) wordt dan bepaald als de energetische som van twee termen, die gewogen zijn met de kans dat een schot (van bron b voor meteorologische situatie m) respectievelijk wel en niet gehoord wordt:
| (6.1) |
kperiode is hierbij de kans dat het schietgeluid in de dag-, avond of nachtperiode hoorbaar is. Deze kans hangt onder andere af van het geluidniveau van het schietgeluid, de omgeving waarin men zich bevindt en de aard van de activiteiten waar men mee bezig is.
Bovenstaande formule kan ook worden geschreven als
LEs,periode(b.m) = LAE(b,m) + C(b,m) | (6.2) |
met
| (6.3) |
C(b,m) is hierbij dan de correctie om een deelbijdrage van schietgeluid om te rekenen naar een even hinderlijk niveau van wegverkeersgeluid. Gemakkelijk is in te zien dat C(b,m) = Pimp + Plf(b,m) voor kperiode = 1, en C(b,m) = 0 voor kperiode = 0.
De kans kperiode wordt bepaald volgens de formule:
| (6.4) |
waarin voor een periode de z-waarde wordt bepaald volgens de formule:
zperiode = a1 + a2LAE(b,m) + a3ΔL'[LAE(b,m) − a4] | (6.5) |
zie voor de berekening van ΔL' hoofdstuk 3. De coëfficiënten a1 t/m a4 zijn hierbij afhankelijk van de periode en zijn weergegeven in tabel 6.1.
Dag | Avond | Nacht | |
|---|---|---|---|
a1 | −5,3 | −5,3 | −0,413 |
a2 | 0,155 | 0,155 | 0,063 |
a3 | 0,002 | 0,002 | 0,0054 |
a4 | 45 | 45 | 25 |
Formule (6.4) beschrijft de gestandaardiseerde cumulatieve normaalverdeling. In standaard statistiekboeken zijn tabellen opgenomen die voor willekeurige waarden van z de uitkomst van deze integraal geven.